MODELO DEPREDADOR-PRESA (Lotka-volterra)
Anuncio

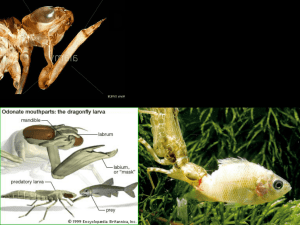
UNIVERSIDAD DE ORIENTE UNIDAD DE CURSOS BASICOS AREA DE MATEMATICA MODELO DEPREDADOR-PRESA (Lotka-volterra) PROF.CRISTIAN CASTILLO MATEMATICAS IV INTEGRANTES: *ESCOBAR, LUISANA *RAMOS, ANA TERESA *SALAZAR, MARIA *SANCHEZ, CARMINE MODELO DEPREDADOR-PRESA (Lotka-volterra) EL PROBLEMA DEPREDADOR-PRESA: UN PROBLEMA EN ECOLOGÍA Hay muchas situaciones en la naturaleza donde una especie animal se alimenta de otra, la cual a su vez se alimenta de otras cosas, ejemplo: Los zorros se alimentan de conejos, los cuales a su vez se alimentan de zanahorias. En este caso los zorros se denominan depredadores y los conejos serán las presas. Teóricamente, el depredador puede destruir toda la presa, de modo que esta última llegue a extinguirse. Sin embargo, si esto ocurre esta también se extinguirá, puesto que depende de la presa para su existencia. De esta forma se desarrolla un ciclo en el cual la presa puede ser abundante y los depredadores pocos, y luego, debido a la abundancia de presa, la población de depredadores aumenta, disminuyendo la primera, y el ciclo continua. GRAFICA DEL MODELO Un problema importante en la ecología es investigar la cuestión de coexistencia de las dos especies, y decidir lo que debería hacer la humanidad, si algo puede, para preservar el balance ecológico. Para responder esto y otras cuestiones relacionadas, es natural buscar una formulación matemática de este problema DEPREDADORPRESA. FORMULACIÓN MATEMÁTICA Asumamos la siguiente notación: X = Número de presas en cualquier tiempo t. Y = Número de depredadores en cualquier tiempo t. Si no hubieran depredadores: Similarmente, si no hubiera presa: Ambas ecuaciones deben modificarse de manera de que exista interacción entre las especies y para ello se incluye un término de interacción que dependa de x y y, quedando: Ecuación para el número de presas: Ecuación para el número de depredadores: Este sistema no se puede resolver en términos de funciones elementales, puesto que, para la solución del mismo es necesario emplear METODOS NUMERICOS o programas matemáticos. Sin embargo esta afirmación no es válida cuando X(t)=0 y Y(t)=0. EJEMPLO Suponga que el sistema de ecuaciones diferenciales describen un modelo particular del depredador (y) y de la presa(x).Determinar la solución y la gráfica: Debido a que solo podemos resolver las ecuaciones cuando x=0 y y=0, se desprecian los segundos términos de las ecuaciones, quedando las mismas: Acomodando las ecuaciones nos quedan dos ecuaciones homogéneas: Soluciones