es una reparametrización de S
Anuncio
Unidad 3 Integral de Supercie
3.3 Independencia de la Parametrización
Independencia de la parametrización
Denición 1. Sea f
: D ⊂ R2 → R3 con S = f (D) una supercie parametrizada , y sea ϕ : D → D una
función biyectiva denida en D ⊂ R2 la cual es tipo I y II a la vez, de clase c1 .
Decimos que la función
f ◦ g : D ⊂ R2 → R3
es una reparametrización de S
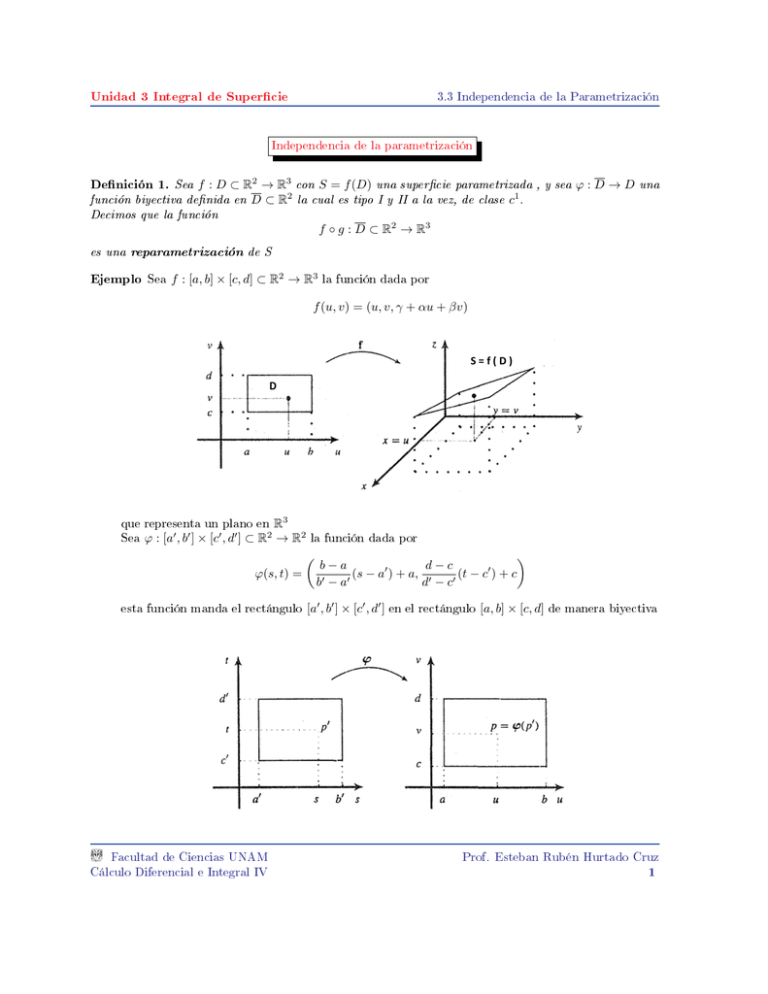
Ejemplo Sea f
: [a, b] × [c, d] ⊂ R2 → R3 la función dada por
f (u, v) = (u, v, γ + αu + βv)
que representa un plano en R3
Sea ϕ : [a0 , b0 ] × [c0 , d0 ] ⊂ R2 → R2 la función dada por
ϕ(s, t) =
b−a
d−c
0
0
(s − a ) + a, 0
(t − c ) + c
b0 − a0
d − c0
esta función manda el rectángulo [a0 , b0 ] × [c0 , d0 ] en el rectángulo [a, b] × [c, d] de manera biyectiva
Facultad de Ciencias UNAM
Cálculo Diferencial e Integral IV
Prof. Esteban Rubén Hurtado Cruz
1
Unidad 3 Integral de Supercie
3.3 Independencia de la Parametrización
La función g : f ◦ ϕ : [a0 , b0 ] × [c0 , d0 ] → R3 dada por
b−a
d−c
0
0
g(s, t) = (f ◦ ϕ)(s, t) = f (ϕ(s, t)) = f
(s − a ) + a, 0
(t − c ) + c =
b0 − a0
d − c0
b−a
d−c
b−a
d−c
0
0
0
0
(s
−
a
)
+
a,
(t
−
c
)
+
c,
(s
−
a
)
+
a
α
+
(t
−
c
)
+
c
+
γ
b0 − a0
d 0 − c0
b0 − a 0
d0 − c0
tiene la misma imagen que f, es inyectiva de clase c1 . Se trata entonces de una función que parametriza a la supercie S, es decir
S = f ([a, b] × [c, d]) = g([a0 , b0 ] × [c0 , d0 ])
Si g(s, t) = (f ◦ ϕ)(s, t) entonces g es una reparametrización de f
en tal caso se tiene que ϕ(s, t) = (ϕ1 (s, t), ϕ2 (s, t)) en donde u = ϕ1 (s, t) y v = ϕ2 (s, t) ∴ se tiene que
g 0 (s, t) = f 0 (ϕ(s, t)) · ϕ0 (s, t) es decir
∂g
ϕ1
∂f
ϕ2
∂f
(s, t) =
(s, t) ·
(ϕ(s, t)) +
(s, t) ·
(ϕ(s, t))
∂s
∂s
∂u
∂s
∂v
Facultad de Ciencias UNAM
Cálculo Diferencial e Integral IV
Prof. Esteban Rubén Hurtado Cruz
2
Unidad 3 Integral de Supercie
3.3 Independencia de la Parametrización
∂g
ϕ1
∂f
ϕ2
∂f
(s, t) =
(s, t) ·
(ϕ(s, t)) +
(s, t) ·
(ϕ(s, t))
∂t
∂t
∂u
∂t
∂v
∴
∂g
∂g
ϕ1
∂f
ϕ2
∂f
ϕ1
∂f
ϕ2
∂f
(s, t)× (s, t) =
(s, t)· (ϕ(s, t))+ (s, t)· (ϕ(s, t))× (s, t)· (ϕ(s, t))+ (s, t)· (ϕ(s, t))
∂s
∂t
∂s
∂u
∂s
∂v
∂t
∂u
∂t
∂v
ϕ
∂f
ϕ2
ϕ1
ϕ2
∂f
1
(s, t) ·
(s, t) −
(s, t) ·
(s, t)
(ϕ(s, t)) ×
(ϕ(s, t))
=
|{z}
∂s
∂t
∂t
∂s
∂u
∂v
→
−
→
−
→
−
−
−
−
α→
a +β b ×γ →
a +δ b =(αγ−βδ)(→
a×b)
donde
∂g
∂g
(s, t) ×
(s, t) = Ng
∂s
∂t
ϕ
ϕ2
ϕ1
ϕ2
(s, t) −
(s, t) ·
(s, t) = Jg (s, t)
∂s
∂t
∂t
∂s
∂f
∂f
(ϕ(s, t)) ×
(ϕ(s, t)) = Nf
∂u
∂v
1
(s, t) ·
∴
Z Z
a(s) =
Ng = Jg (s, t)Nf (u, v)
Z Z
∂(ϕ1 , ϕ2 ) kNf (u, v)k dudv
=
kN
(ϕ(s,
t))k
f
∂(s, t) |{z}
e
D
D
(u,v)=ϕ(s,t)
∴ el área de la superfície no depende de la parametrización
Ejemplo.-Vamos a calcular el área de la superfície z = x2 + y 2 sobre la región
D = {(x, y) ∈ R2 |x2 + y 2 ≤ 1}
Facultad de Ciencias UNAM
Cálculo Diferencial e Integral IV
Prof. Esteban Rubén Hurtado Cruz
3
Unidad 3 Integral de Supercie
3.3 Independencia de la Parametrización
Para ello parametrizamos la superfície z = x2 + y 2 de la siguiente manera r(x, y) = (x, y, x2 + y 2 ) y por
lo tanto
∂r
= (1, 0, 2x)
∂x
∂r
= (0, 1, 2y)
∂y
bi b
b
j
k
∂r
∂r
×
= 1 0 2x = (−2u, −2v, 1)
∂x ∂y 0 1 2y ∴
∴ el área es
Z Z Z Z p
Z 2π Z 1 p
∂r
∂r 2 + 4y 2 + 1dudv
dA =
×
4x
=
4r2 + 1rdrdθ
|{z} 0
∂y D ∂x
0
D
P olares
1
8
=
|{z}
u=4r 2 +1
r=0→u=1
du=8r
r=1→u=5
5
2π Z
Z
√
1
0
1
ududθ =
8
2π Z
0
2 3 5
u2 0
3
1
dθ =
8
2π
Z
0
2 3
π 3
5 2 − 1 dθ =
52 − 1
3
6
Ahora vamos a dar una reparametrización de D de la siguiente forma, proponemos
e = {(s, t) ∈ R2 |s2 + t2 ≤ 1 } de esta manera si
D
2
s2 + t2 ≤
1
⇒ 2s2 + 2t2 ≤ 1 ⇒ s2 + 2st + t2 + s2 − 2st + t2 ≤ 1 ⇒ (s + t)2 + (s − t)2 ≤ 1
2
∴ podemos tomar u = s + t y v = (s − t) y por tanto nuestra reparametrización quedaría
g(s, t) = (s + t, s − t, 2s2 + 2t2 )
donde
∂g
= (1, 1, 4s)
∂s
∂g
= (1, −1, 4t)
∂t
∂g ∂g ×
=
∂s
∂t
∴
bi b
j
1 1
1 −1
b
k
4s
4t
= (4t + 4s, 4s − 4t, −2)
∴ el área es
Z Z p
Z Z p
Z Z ∂g ∂g 2 + (4s − 4t)2 + (−2)2 dsdt =
dA =
(4s
+
4t)
32t2 + 32s2 + 4dsdt
×
∂t D
D
D ∂s
2π
Z
= 2
|{z}
P olares
=
|{z}
u=8r 2 +1
du=16r
1 →u=5
r=0→u=1
r= √
2
2
8
Z
0
2π
Z
5
√
1
Facultad de Ciencias UNAM
Cálculo Diferencial e Integral IV
1
ududθ =
4
0
1
√
2
Z
p
8r2 + 1rdrdθ
0
Z
0
2π
2 3 5
u2 0
3
1
dθ =
4
Z
0
2π
2 3
π 3
5 2 − 1 dθ =
52 − 1
3
6
Prof. Esteban Rubén Hurtado Cruz
4











