Introducción Toda superficie cuya temperatura sea mayor que la del

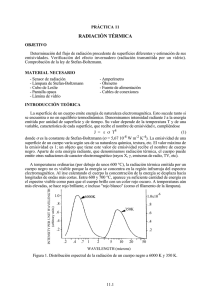
Trabajo de laboratorio Nro 1: “Determinación de la constante de Planck mediante el análisis de la radiación del cuerpo negro” Introducción
Toda superficie cuya temperatura sea mayor que la del cero absoluto, emite radiación
térmica. En los diversos procesos que originan la radiación, se emite un espectro completo
de longitudes de onda. Un cuerpo que tiene la propiedad de absorber toda la radiación que
incide sobre él, recibe el nombre de cuerpo negro y por ende, emite todo lo que incide. Así,
un cuerpo negro es el absorbente y el emisor más eficiente. Si se mide la intensidad de
radiación emitida por un cuerpo negro en función de la longitud de onda se obtienen curvas
como las siguientes:
A medida que aumenta la temperatura (T) del cuerpo la longitud de onda (máx ) a la cual se
encuentra el máximo de intensidad disminuye lo que hace que vayamos viendo que el
objeto cambia de color. Del análisis de estas curvas se obtuvieron dos leyes importantes:
 La ley de desplazamiento de Wien (Premio Nobel 1911):
máxT = constante
 Ley de Stefan-Boltzmann, la intensidad total es proporcional a la cuarta potencia de
la temperatura absoluta:
R  T4
donde R es la radiación térmica emitida por un objeto a una temperatura T,  es la
constante de Stefan-Boltzmann y es igual a (5, 670400 ± 0, 000040) × 10−8Wm−2K−4
y T es la temperatura absoluta del objeto en consideración.
Los trabajos de Stefan, Boltzmann y Wien, entre otros, sirvieron como base para que Lord
Rayleigh y Sir James Jeans, llegaran a una expresión desarrollada en términos de la física
clásica para la radiación de cuerpo negro, la cual estuvo de acuerdo con los resultados
experimentales solo parcialmente. La discrepancia fue resuelta poco tiempo después por
Max Planck en términos de una nueva concepción de la energía asociada al campo
electromagnético, lo que dio origen a la física cuántica.
1
La ley de Planck conlleva a la siguiente expresión para la distribución de frecuencias para
la intensidad de radiación de un cuerpo negro a una temperatura T:
donde
es la cantidad de energía por unidad de área, unidad de tiempo y unidad de
ángulo sólido emitida en el rango de frecuencias entre y
, c, es la velocidad de la
-23
luz, k la constante de Boltzmann (1.38 x 10 J/K) y h la constante de Planck.
Podemos expresar el cociente de dos intensidades medidas a la misma frecuencia para dos
temperaturas diferentes T 1 y T 2, de la siguiente forma:
hv
kT 1
I (v, T 2) e  1
 hv
I (v, T 1)
e kT 2  1
Para las temperaturas con las que vamos a trabajar exp(h/kT)>>1, y en estas condiciones,
la ecuación anterior puede expresarse como:
 h
I (v, T 2)
 exp
I (v, T 1)
 k
 1 1 
   

 T1 T2  
En este trabajo de laboratorio usaremos esta expresión para determinar la constante de
Planck a partir de la medida de la intensidad de radiación para una frecuencia fija.
Procedimiento
Como cuerpo negro se utilizará una lámpara con un filamento de tungsteno de 40 watts de
potencia alimentada por una fuente con resistencia variable (0-240V). Como detector de la
radiación se utilizará un diodo polarizado en forma inversa con respuesta espectral entre
900 y 1000 nm, a este diodo se le acopla un amplificador que da como señal de salida una
diferencia de tensión proporcional a la corriente inversa que circula por el circuito y en
consecuencia proporcional a la intensidad de radiación incidente en el fotodiodo. Se
utilizarán además, dos multímetros para medir la corriente y tensión en el filamento para
luego obtener la resistencia del filamento y de ahí la temperatura del mismo.
La lámpara y el diodo detector se colocan enfrentados (a unos 20 cm) dentro de un
recipiente opaco para aislar al sistema de la radiación ambiental.
1. Con la lámpara apagada tomar lectura de: la temperatura ambiente, la resistencia del
filamento y la tensión de salida del fotodiodo (Vdiodo).
2. Variar la corriente que circula por la lámpara e ir registrando los valores de:
corriente, tensión (en la lámpara) y tensión del fotodiodo. Sugerencia: puede variar
los valores de tensión en la lámpara cada 10 V.
2
3. Determinar la resistencia del filamento (para 5cada medida) y a partir de ésta calcular
la T del mismo usando la relación
 R 6

T  T 0 
 R0 
4. Determine h a partir del análisis de los datos (ayuda: haga uso de la ecuación que da
el cociente relativo de las intensidades tomando como T1 la temperatura ambiente y
como T la temperatura variable y recuerde que Vdiodo es proporcional a la intensidad
de radiación incidente en el fotodiodo).
Esquema breve del dispositivo
I ( 0 , T ) ~ i (T )
A
V ~i
V
V
caja negra
Características del diodo BP104
3
.