La Radiación de cuerpo negro
Anuncio

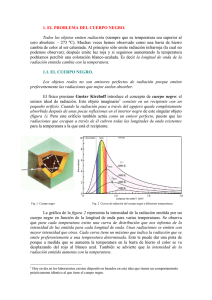
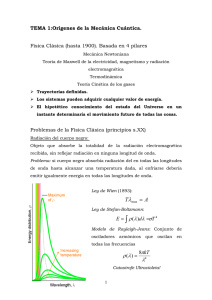
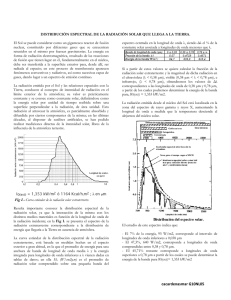
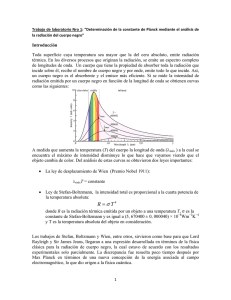
La Radiación de cuerpo negro. Alumno: Ernesto Espíndola Ramos La superficie de todo cuerpo con temperatura mayor a cero absoluto emite energía térmica en forma de ondas electromagnéticas, esto es debido a la aceleración de cargas eléctricas debido al movimiento térmico, en los muy diversos procesos de aceleración, se emite un espectro completo de longitudes de onda. La cantidad total de energía emitida por segundo y por 𝑐𝑚2 (Intensidad) es directamente proporcional a la temperatura (a mayor temperatura, mayor es la energía de la radiación emitida), esta relación se conoce como ley de Stefan-Boltzmann (la cual en sus inicios era una ecuación empírica): 𝐼 = 𝜎𝑒𝑇 4 𝐼=intensidad total emitida, 𝜎=constante de Stefan Boltzmann, 𝑒=emisividad Un cuerpo negro es aquel cuerpo que tiene la propiedad de absorber toda la radiación que incide sobre el (en la naturaleza se encuentran cuerpos aproximados a un cuerpo negro). De acuerdo con la lay de Kirchoff de la radiación térmica ( un cuerpo en equilibrio termodinámico, tiene ua emisividad igual a su absorbancia), un cuerpo negro, que es el absorbente más eficiente, también es el radiador más eficiente. De acuerdo con la ley de Stefan-Boltzmann, la distribución espectral de la radiación de un cuerpo negro ( 𝐼𝑇 (𝜆)) sólo depende de su temperatura y no de su estructura interna. Las primeras medidas de estas cantidades ( 𝐼𝑇 (𝜆)) están asociadas con los nombres de Lummer y Pringsheim, observándose el siguiente comportamiento: La integral de 𝐼𝑇 (𝜆) a una temperatura T está dada por 𝐼 = 𝜎𝑒𝑇 4 La ley de Rayleigh-Jeans es un modelo deducido de las teorías de la física clásica para explicar la distribución espectral de la radiación de un cuerpo negro, la radiación del cuerpo a una longitud de onda dada es: 𝐵𝜆 (𝑇) = 2𝐶𝐾𝑇 𝜆4 (ley de Rayleigh-Jeans) Esta ley predice una producción de energía infinita a longitudes de onda muy pequeñas. Si comparamos esto con lo observado con el experimento, notamos lo siguiente: Puede observarse que esta ley no predice lo observado cuando se trata esencialmente de longitudes de onda cortas, este comportamiento para longitudes de onda cortas se conoce como la catástrofe ultravioleta. Planck pudo eliminar esta discrepancia a través del postulado siguiente: Cualquier entidad física cuya única “coordenada” efectúa oscilaciones armónicas simples (esto es, que sea una función sinusoidal del tiempo), solamente puede tener una energía total que satisface la relación: 𝜖 = 𝑛ℎ𝜈, 𝑛 = 0,1,2,3, … Donde 𝜈 es la frecuencia de oscilación y ℎ es una constante universal. Haciendo los cálculos correspondientes tomando en cuenta que se satisfaga el postulado de Planck llegamos a la siguiente expresión: 𝐼(𝜈, 𝑇) = 2ℎ𝜈 3 1 2 𝐶 exp(ℎ𝜈⁄ ) − 1 𝐾𝑇 La cual se ajusta a los datos obtenidos experimentalmente. El triunfo del postulado de Planck al conducir a la explicación teórica del espectro del cuerpo negro nos hace aceptar tentativamente su validez, a menos que se demuestre algún día que lleva a conclusiones que discuerdan con el experimento. Referencias: Fundamentos de física moderna. Robert M. Eisberg. Primera edición. Ed. Limusa. Capitulo 2. Ley de Kirchhoff de la radiación térmica: http://es.wikipedia.org/wiki/Ley_de_Kirchhoff_de_la_radiación_térmica Cuerpo negro: http://es.wikipedia.org/wiki/Cuerpo_negro