Desplazamiento vertical de una gráfica Desplazamiento horizontal

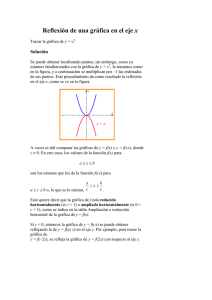
Desplazamiento vertical de una gráfica
Trazar la gráfica de f:
(a) f(x) = x2 (b) f(x) = x2 +4 (c) f(x) = x2 –4
Solución
Se trazarán todas las gráficas en el mismo plano coordenado.
(a) Como f(–x) = (–x)2 = x2 = f(x),
la función f es par, y por consiguiente, su gráfica es simétrica con
respecto al eje y. Algunos de los puntos de esta gráfica de y = x2
son (0, 0), (1, 1), (2, 4) y (3, 9).
Al trazar una curva uniforme que pase por esos puntos, y
reflejándola luego en el eje y, se obtiene el esquema de la figura
siguiente.
La gráfica es una parábola con vértice en el origen, cóncava hacia
arriba.
(b) Para el trazo de la gráfica de y = x2 + 4, se suma 4 a la
ordenada de cada punto de la gráfica de y = x2 Esto es, se
desplaza la gráfica del inciso (a) 4 unidades hacia arriba, como se
ve en la figura.
(c) Para trazar la gráfica de y = x2 –4, se resta 4 a las ordenadas de
y = x2, esto es, se desplaza la gráfica del inciso (a) 4 unidades
hacia abajo.
Desplazamiento horizontal de una
gráfica
Trazar la gráfica de f:
(a) f(x) = (x – 4)2
(b) f(x) = (x + 2)2
Solución
La gráfica de y = x2 aparece en la figura.
(a) Al desplazar la gráfica de y = x2, 4 unidades hacia la derecha,
se tiene la de y = (x –4)2, que se ve en la figura.
(b) Al trasladar la gráfica de y = x2, 2 unidades hacia la izquierda,
se obtiene la de y = (x + 2)2, que también se ve en la figura.