Hoja de ejercicios n°2-C Ejercicios de simulación de sistemas
Anuncio
DEPARTAMENTO DE
SISTEMAS Y CONTROL
INTRODUCCIÓN AL CONTROL INDUSTRIAL
Año 2014
Hoja de ejercicios n2-C
Ejercicios de simulación de sistemas. Scilab. Scicos.
Obs: El objetivo de esta hoja de ejercicios es introducir el estudiante en la utilización de programas
numéricos , como el Scilab, en el análisis de problemas de control. El conocimiento de programas
similares, como el Matlab, es muy recomendable. Se sugiere la lectura de los manuales
correspondientes para los estudiantes sin experiencia (www.scilab.org).
1) Linealización.
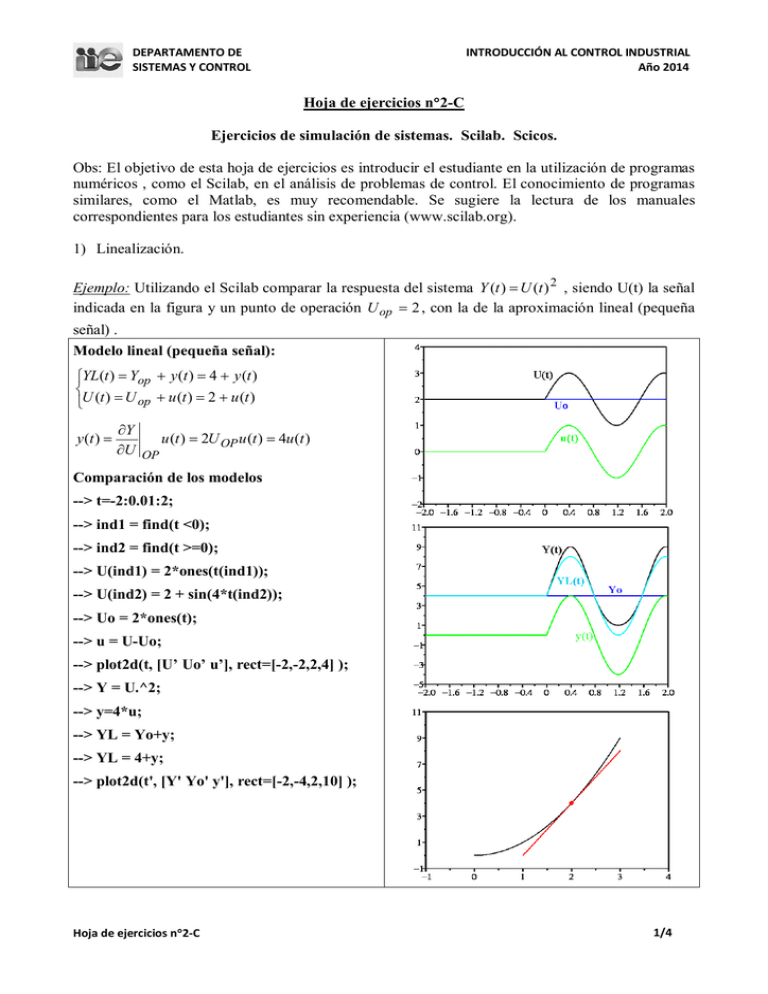
Ejemplo: Utilizando el Scilab comparar la respuesta del sistema Y (t ) U (t ) 2 , siendo U(t) la señal
indicada en la figura y un punto de operación U op 2 , con la de la aproximación lineal (pequeña
señal) .
Modelo lineal (pequeña señal):
YL(t ) Yop y (t ) 4 y (t )
U (t ) U u (t ) 2 u (t )
op
y (t )
Y
u (t ) 2U OP u (t ) 4u (t )
U OP
Comparación de los modelos
--> t=-2:0.01:2;
--> ind1 = find(t <0);
--> ind2 = find(t >=0);
--> U(ind1) = 2*ones(t(ind1));
--> U(ind2) = 2 + sin(4*t(ind2));
--> Uo = 2*ones(t);
--> u = U-Uo;
--> plot2d(t, [U’ Uo’ u’], rect=[-2,-2,2,4] );
--> Y = U.^2;
--> y=4*u;
--> YL = Yo+y;
--> YL = 4+y;
--> plot2d(t', [Y' Yo' y'], rect=[-2,-4,2,10] );
Hoja de ejercicios n2-C
1/4
DEPARTAMENTO DE
SISTEMAS Y CONTROL
INTRODUCCIÓN AL CONTROL INDUSTRIAL
Año 2014
Ejemplo: Utilizando el Scicos comparar la respuesta del sistema Y (t ) U (t ) 2 , siendo U(t) la señal
indicada en la figura y un punto de operación U op 2 , con la de la aproximación lineal (pequeña
señal) .
Ejercicio: Para los sistemas a continuación comparar las respuestas del modelo no lineal y la
aproximación utilizando el modelo lineal (pequeña señal).
a) Y (t ) U (t ) 3 2 cos(U (t )); U o
Posibles entradas:
a1) U (t ) 0.05 sen(t ).
4
a2) U (t )
0.2 sen(t ).
4
Hoja de ejercicios n2-C
4
b)
d 2 Y (t )
dt 2
Y (t ) 3
dY (t )
Y (t ) U (t )
dt
Puntos de equilibrio: U o 3 2 y U o 3 0.5
Entrada: U (t ) U o
Uo
1(t ). (onda cuadrada)
5
2/4
DEPARTAMENTO DE
SISTEMAS Y CONTROL
INTRODUCCIÓN AL CONTROL INDUSTRIAL
Año 2014
2) Respuesta en el dominio del tiempo. Transitorios.
dy (t )
Ejemplo: Simular la respuesta del sistema
5 y (t ) 10u (t ) (condiciones iniciales nulas) a una
dt
entrada escalón unitario, utilizando el Scilab.
Transformada de Laplace:
sY ( S ) 5Y ( s ) 10U ( s )
Y ( s)
10
G( s)
U (s)
s5
--> s = poly(0,’s’);
--> G = 10/(s+5);
--> sys = syslin(‘c’,G);
--> t = 0:0.01:1;
--> y = csim(‘step’,t,sys);
--> plot2d(t, [ones(t)’ y’], rect=[0,0,1,2] );
dy (t )
5 y (t ) 10u (t ) (condiciones iniciales nulas) a una
dt
entrada escalón unitario, utilizando el Scicos.
Ejemplo: Simular la respuesta del sistema
Ejercicio: Para los sistemas graficar la respuesta a una entrada escalón unitario (condiciones
iniciales nulas).
a)
d 2 y (t )
dt 2
dy (t )
2 n
22 y (t ) K 22 u (t )
dt
b)
dY (t )
dU (t )
2Y (t )
4U (t )
dt
dt
Juego de parámetros:
a1) K 1; 1; n 1
a2) K 0.5; 0.25; n 2
Hoja de ejercicios n2-C
3/4
DEPARTAMENTO DE
SISTEMAS Y CONTROL
INTRODUCCIÓN AL CONTROL INDUSTRIAL
Año 2014
3) Respuesta en el dominio de la frecuencia. Diagramas de Bode.
dy (t )
y (t ) u (t ) .
dt
Realizar la simulación de la respuesta a una señal de entrada u (t ) 2 sen( 0.5t ) cos(10t )
(condiciones iniciales nulas). Calcular la salida en régimen (yss(t)).
Ejemplo: Utilizando el Scilab, realizar los diagramas de Bode del sistema
Función de transferencia:
sY ( S ) Y ( s ) U ( s )
Y ( s)
1
G (s )
U ( s)
s 1
Diagramas de Bode
--> s = poly(0,’s’);
--> G = 1/(s+1);
--> sys = syslin(‘c’,G);
--> bode(G);
Simulación
--> deff('z=input(t)','z=2*sin(0.5*t)+cos(10*t)');
--> u=input(t);
--> y=csim(input,t,sys);
--> plot2d(t',[u' y']);
Cálculo de yss
--> f = [0.5 10]*(1/(2*%pi));
--> [frq, repf]=repfreq(sys,f);
--> mod = abs(repf)
mod =
!
.8944272
.0995037 !
--> ang=atan(imag(repf),real(repf));
ang =
! - .4636476 - 1.4711277 !
yss(t) = 1.79sen(0.5t-0.46) + 0.1cos(10t-1.47)
Ejercicio: Utilizando el Scilab, realizar los diagramas de Bode de los sistemas a continuación.
Simular la respuesta a las entradas indicadas y comparar con la respuesta en régimen teórica.
a)
dy (t )
10 y (t ) 20u (t )
dt
u (t ) sen(t ) cos(10t )
Hoja de ejercicios n2-C
d 2 y (t )
b)
dt 2
0. 2
dy (t )
y (t ) u (t )
dt
u (t ) 2 sen( 0.1t ) 0.5 sen(t ) 0.1 cos(10t )
4/4