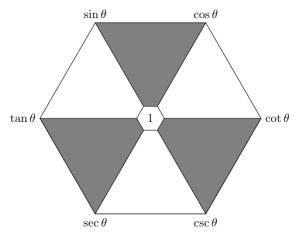
Trigonometric Identities

sin θ = y
cos θ = x
tan θ = y/x
definitions
sin θ = y
csc θ = 1/y
cos θ = x
sec θ = 1/x
tan θ = y/x
cot θ = x/y
double angle
(x, y)
θ
sin(2θ ) = 2 sin θ cos θ
cos(2θ ) = cos2 θ − sin2 θ
tan(2θ ) =
sec θ = 1/xidentities
pythagorean
2
half angle
2
sin θθ=+x/y
cos θ = 1
cot
tan2 θ + 1 = sec2 θ
cot2 θ + 1 = csc2 θ
1
sin θ
1
tan θ
sin θ
cos θ
sin(−θ ) = − sin(θ )
cos θ
cot θ =
cos(−θ )sin
= θcos(θ )
negatives
tan θ =
tan(−θ ) = − tan(θ )
csc(−θ ) = − csc(θ )
cofunctions
sec(−θ ) =
sec θ =
1
cos θ
tan θ =
1
sec θ =
cos θ
cot θ =
1
sin θ
1
cot θ =
tan θ
reciprocals
csc θ =
csc θ =
sin θ
cos θ
tan
θ
1 − cos θ
sin θ
=
=
2
sin θ
1 + cos θ
power reduction
cos θ
cot θ =
sin θ
sin(−θ ) = − sin(θ )
sin2 θ =
1 − cos(2θ )
2
cos(−θ ) = cos(θ )
cos2 θ =
1 + cos(2θ )
2
tan(−θ ) = − tan(θ )
tan2 θ =
1 − cos(2θ )
1 + cos(2θ )
csc(−θ ) = − csc(θ )
π

sec(−θ
)=
)θ
sin
−
θ sec(θ
= cos
2
 cot(θ )
π ) = −
cot(−θ
− θ = sin θ
cos
2
π

tan
− θ = cot θ
2
π

csc
− θ = sec θ
2
π

sec
− θ = csc θ
2

π
cot
− θ = tan θ
2
sec(θ )
π

cot(−θ
)=
cot(θ
sin
−
θ −=
cos θ)
2
π

cos
− θ = sin θ
2
π

tan
− θ = cot θ
2
π

csc
− θ = sec θ
2


additionπ
sec
− θ = csc θ
sin(α2+ β ) = sin α cos β + cos α sin β
π

cot +−βθ) ==cos
tanαθcos β − sin α sin β
cos(α
2
tan(α + β ) =

θ
1 − cos θ
sin = ±
2
2

θ
1 + cos θ
cos = ±
2
2
tan α + tan β
1 − tan α tan β
sum to product




α +β
α −β
sin α + sin β = 2 sin
cos
2
2

 

α +β
α −β
sin α − sin β = 2 cos
sin
2
2




α +β
α −β
cos
cos α + cos β = 2 cos
2
2

 

α +β
α −β
cos α − cos β = −2 sin
sin
2
2
product to sum
1
sin α sin β = [cos(α − β ) − cos(α + β )]
2
1
cos α cos β = [cos(α + β ) + cos(α − β )]
2
1
sin α cos β = [sin(α + β ) + sin(α − β )]
2
Trigonometric Identities
csc θ = 1/y
2 tan θ
1 − tan2 θ