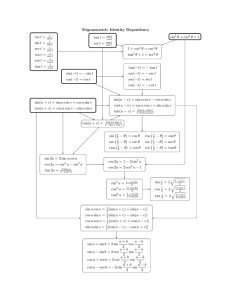
Basic trigonometric identities Common angles

Basic trigonometric identities
Common angles
Degrees
0◦
Radians
0
sin
0
cos
1
tan
0
30◦
π
6
1
2
√
3
2
√
3
3
45◦
π
4
√
2
2
√
2
2
1
Reciprocal functions
cot x =
1
tan x
csc x =
1
sin x
sec x =
1
cos x
Even/odd
sin(−x) = − sin x
cos(−x) = cos x
tan(−x) = − tan x
Pythagorean identities
sin2 x + cos2 x = 1
1 + tan2 x = sec2 x
1 + cot2 x = csc2 x
1
60◦
π
3
√
3
2
1
2
√
3
90◦
π
2
1
0
Cofunction identities
π
2
π
cos(
2
π
tan(
2
π
cot(
2
π
sec(
2
π
csc(
2
sin(
− x) = cos x
− x) = sin x
− x) = cot x
− x) = tan x
− x) = csc x
− x) = sec x
Sum and difference of angles
sin(x + y) = sin x cos y + cos x sin y
sin(x − y) = sin x cos y − cos x sin y
cos(x + y) = cos x cos y − sin x sin y
cos(x − y) = cos x cos y + sin x sin y
tan(x + y) =
tan x + tan y
1 − tan x tan y
tan(x − y) =
tan x − tan y
1 + tan x tan y
Double angles
sin(2x) = 2 sin x cos x
cos(2x) = cos2 x − sin2 x
= 2 cos2 x − 1
= 1 − 2 sin2 x
tan(2x) =
2 tan x
1 − tan2 x
2
Half angles
r
x
1 − cos x
sin = ±
2
2
r
x
1 + cos x
cos = ±
2
2
tan
x
1 − cos x
=
2
sin x
=
sin x
1 + cos x
Power reducing formulas
sin2 x =
1 − cos 2x
2
cos2 x =
1 + cos 2x
2
tan2 x =
1 − cos 2x
1 + cos 2x
Product to sum
1
cos(x − y) − cos(x + y)
2
1
cos x cos y =
cos(x − y) + cos(x + y)
2
1
sin x cos y =
sin(x + y) + sin(x − y)
2
sin x sin y =
tan x tan y =
tan x + tan y
cot x + cot y
tan x cot y =
tan x + cot y
cot x + tan y
3
Sum to product
sin x + sin y = 2 sin
sin x − sin y = 2 cos
x + y 2
x + y cos
x − y 2
x − y sin
2
2
x − y x + y cos
cos x + cos y = 2 cos
2
2
x + y x − y cos x − cos y = −2 sin
sin
2
2
tan x + tan y =
sin(x + y)
cos x cos y
tan x − tan y =
sin(x − y)
cos x cos y
Source
http://evgenii.com/blog/basic-trigonometric-identities
Basic triginometric identities by Evgenii Neumerzhitckii is licensed under a Creative Commons Attribution 4.0 International License.
4