Aplicaciones trigonometría
Anuncio

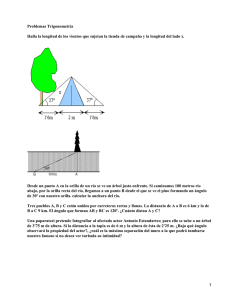
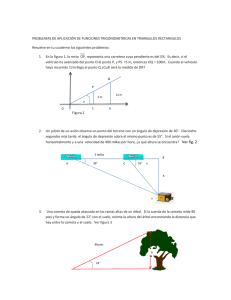
1 Universidad Nacional Facultad de Ciencias Exactas y Nayurales Escuela de Matemática MAX-084 Prof. Jendry Arguedas Flatts Aplicaciones trigonometría 1. Para determinar la longitud del lago Angosto, un topógrafo desea medir la distancia entre los puntos A y C en orillas opuestas del lago. Desde el punto C el topógrafo mide una distancia de 250m hasta un punto B, de manera que BC es perpendicular a la línea visual entre A y C, mediante un transito (instrumento que mide ángulos) el topópgrafo encuentra que la medida del ángulo B es de 82 . Determine la distancia entre A y C. R/ aprox 1 779 m 2. Un piloto de un jet de la fuerza naval va a aterrizar en un portaaviones a una altitud de 3000 pies, el piloto observa el portaviones con un ángulo de 15 . ¿Cuál es la distancia horizontal entre el avión y el portaviones? 3. Una antena de TV está colgada en la orilla de la azotea de una casa que tiene una altura de 10m, desde un punto ubicado a 80m de la base de la casa el ángulo de elevación hasta la punta de la antena es de 24 . ¿Qué altura tiene la antena? 4. Para determinar el ancho de un río se tomó como referencia un árbol en la orilla opuesta. EL ángulo de elevación con el cual se observa el árbol (desde la orilla opuesta) es de 32; a 150m de la orilla del río, siguiendo de la medición anterior, la cima del árbol se vería con un ángulo de elevación de 21, ¿Cuál es el ancho del río? 5. Hallar la altura de un aťrbol si el ángulo de elevacion varía de 4,2cm y cada uno de los ángulos de la base mide 27 . Hallar las longitudes de la base y de la altura sobre ella. 6. Desde cierto punto ubicado en el mismo plano de la base de un edificio un observador ve la parte superior del edificio con un ángulo de elevación de 30 , luego camina 50 metros en línea recta alejándose del edificio y, desde este nuevo punto, observa la parte superior del edificio con un ángulo de elevación de 20 . Determinar la altura del edificio. 2 Aplicación de los logaritmos 1. Una población de P = 100000 personas aumenta a P e0,05n , después de n años. Determina la población existente al cabo de 5 años. 2. La fórmula de Ehrenberg W = 2, 4 e1,84h es una ecuación empírica que relaciona el peso W en kilogranos de un niño menor de 12 años, con la estatura h en metros. Estime el peso de un niño de 1,5 m. Encuentre, aproximadamente, la estatura de un niño que pesa 45 kg. 3. La escala de pH expresa la concentración de iones de hidrógeno ([H + ]) con la fórmula pH=− log[H + ]. Si el agua pura tiene un pH de 7. Determine la cantidad de [H + ] para el agua. 4. Si sabemos que la sangre tiene [H + ] = 10−7,4 determine el pH de esta sustancia. 5. Supongiendo que el crecimiento de la población de CR puede aproximarse por medio de una función P (t) = A e0,027t , donde A es la población inicial. Si se sabe que en 1989 la población era de 3 millones, ¿ determine la población de CR en el año 2010?