INSTITUTO TECNOLOGICO DE CHIHUAHUA Tarea Unidad IV
Anuncio

INSTITUTO TECNOLOGICO DE CHIHUAHUA
Tarea Unidad IV
Matematicas IV (ECUACIONES DIFERENCIALES)
Catedrático: Amalia Concepción Aguirre Parres
Zill. edic 5a
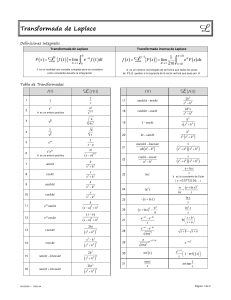
Secc 7.4 En los problemas sig. determinar F(s)
1.-
{t . cos ( 2 . t ) }
2
3.- {t . sinh ( t ) }
.
2t
5.- {t . e . sin ( 6 . t ) }
{1 * t3}
7.-
9.- {e-t * etcos(t)}
Evaluar la transformada de Laplace sin calcular la integral.
t
11
t
τ
{
dτ }
e
0
dτ }
0
t
13.-
t τ
τ.e
15.- {
{
e
τ.
t
cos ( τ ) d τ }
( sin ( τ ) ) d τ }
17.- {t
0
0
Utilizar la ecuación de la transformada inversa de una integral, para encontrar la transformada inversa de:
19 a
-1
1
.
s ( s 1)
{
}
-1
13
{
1
2.
s (s
}
-1
15
1
{
1)
3.
s (s
}
1)
Hallar La transformada de Laplace de las funciones periódicas (ver esquemas en pag. 347 y 348 del libro)
Resolver el problema de valor inicial
27.- y´+ y = t sen(t)
0<= t <π
y(0)= 0
29.- y´´+ 9 y = cos(3t)
y(0)=2
y´(0)=5
31.- y´´+ 16 y= f(t), donde f(t)= cos (4t)
32.- y´´+ y = f(t), donde f(t) = 1
para
para 0 t <
π
2
0 t < π y f(t)=0 para t π ; con y(0)=0 y´(0)=1
t π
y f(t) = sin(t) para t
con y(0) = 1 n y y´(0) = 0
2
Resolver la ecuacion mediante la transformada de Laplace.
t
35.- f ( t )
τ ) . f( τ ) d τ
(t
t
41.-
f( t )
(1
8.
t)
3
0
37.- f ( t )
t. e
t
t
0
t
τ . f( t τ ) d τ
42.-
t
2. f( t )
t
(τ
0
τ
e
0
3
t ) . f( τ ) dτ
e
τ .
f( t
τ ) dτ
38.- f ( t )
t
2.
f ( τ ) . cos ( t τ ) d τ
4. e
t
t
sin ( t )
43.
y( τ ) d τ
y''(t)=1-sin(t)-
y( 0 )
0
0
0
t
f( τ ) d τ
39.- f ( t )
1
0
Secc. 7.5
1.- y ´ - 3y = δ(t - 2)
2.- y ´+ y = δ(t - 1)
7.- y´´ + 2y´ = δ(t - 1)
y(0)=0
9.- y´´ + 4y´+ 5y = δ(t - 2π)
y(0)=2
3.- y ´´+ y = δ(t - 2π)
y(0)=0 y´(0)=1
11.- y´´ + 4y´+ 13y =δ (t - π)+δ (t - 3π)
y(0)=0 y´(0)=1
5.- y ´´+ y = δ(t - π/2)+δ(t - 3π/2)
y(0)=0 y´(0)=0
y(0)=1 y´(0)=0
y(0)=0 y´(0)=0
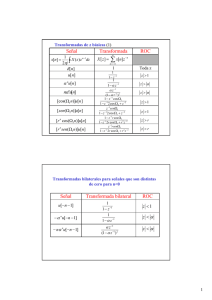
Secc 11.1 Muestre que las funciones son ortogonales.
1.- f1(x) = x,
f2(x) = x2
5.- f1(x)=x,
f2(x)=cosx
[-2,2]
3.- f1(x) = ex,
f2(x) = xex - ex
[-0,2]
[-π/2,π/2]
En los problemas sig. muestre que el conjunto dado de funciones es ortogonal en el intervalo dado
Calcular la norma de cada función del conjunto
7.- {sen(x), sen 3x, sen 5x...} [0,π/2]
9.- {sen(nx)},
n=1,2,3 :
11.- {1, cos
nπ
p
x },
n=1,2,3 : [0,p]
[0,π]
Determinar las series de Fourier de la función en el intervalo dado.
1.- f(x)= 0
π < x < 0 , f(x)=1 0 x < π
9.- f(x)= 0
3.- f(x)= 1
1 < x < 0 , f(x)=x 0 x < 1
13.- f(x)= 1
5.- f(x)= 0
π < x < 0 , f(x)=x2 0 x < π
15.- f(x)= ex
7.- f(x)= x+π
π < x< 0
5< x< 0
, f(x)=sen(x) 0 x < π
, f(x)=1+x 0 x < 5
π < x< π
π < x< π
rev 160503