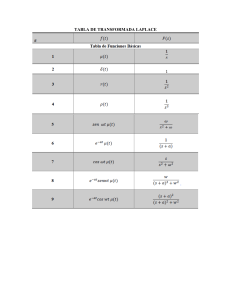
Formulario de transformadas de laplace

L
Transformada de Laplace
Definiciones Integrales
F s 
s
L  f t   lim 
Transformada de Laplace
b
b
e  st f t  dt
es en realidad una variable compleja pero se considera
como constante durante la integración
Tabla de Transformadas
f t 
17
s
n!
s n
2
tn
n es un entero positivo
3
t
π
s
t
π
s
e at
s a
5
6
t ne at
n
es un entero positivo
8
10
coshkt
s
s k
e at cos kt
13
t sen kt
t cos kt
14
15
16
sen kt  kt cos kt
sen kt  kt cos kt
REVISIÓN 5 – 75636.04
21
n
coskt
12
R 
22
 s  a
k
 s  a  k
27
 s  a
s

s k
s k
s

ks
k
k
k
ks
s k
senh kt  sen kt
k
s k
cosh kt  cos kt




28
29
30
31
k s
s k

 coskt
a sen bt  b sen at


ab a  b
s
s
cos bt  cos at
a b
lnt
   ln t 
 ln t  
e  at  e  bt
t
π
e  at  e  bt
πt
a
πt
e a
erf  t 
sen t
t


k
s s k
a
a

 .
 s
 s
s
b
b
 ln s
s


es la constante de Euler
(
ln t


k
s s k
kt  sen kt
25
26
e st F  s  ds
σ iR
L  f t 
24
k

f t 
23
k
s k
πi
σ  iR
σ es un número real elegido de tal forma que todos los polos
F  s  queden a la izquierda de la recta vertical que pasa por σ
20
s
s k
e at sen kt
11

19
k
s k
senhkt
9
18
 s  a
n!
senkt
7
de
L F  s   lim
L  f t 
1
4
f t  
Transformada inversa de Laplace
/ t
)
π   ln s 

s
s
ln s
s
ln s
s
 sb
ln 

 sa
sb  sa
e a
s
es /
  erf  s  
s 
arctan
s
Página 1 de 2
Teoremas y Propiedades Diversas
1
Linearidad
L c f t   c f t     c f t   c F  s   c F  s     c F t 
n n
n n
L e f t   L  f t   F  s 
L F  s  a  e L F  s   e f t 
donde c , c , … cn son constantes
2
Primer teorema de traslación
at

3
Segundo teorema de traslación
 ,
t a
donde la función escalón unitario es
U t  a   ,
t a
4
Función multiplicada por t n
(derivada de transformada)
5
Función dividida entre t
(integral de transformada)
6
Transformada de derivada


L t

 as
n

f t    
 f t  

t 
L 


s

n
t t  a
F  s  ds
L  dfdt   sF  s   f 




Teorema de convolución

donde la integral de convolución es
9
f *g
t
f  τ  g  t  τ  dτ
Transformada de una función
periódica con periodo T tal que
f t  T   f t 
10 Transformada de una función
periódica con periodo T tal que
g t  T    g t 
11 Función delta de Dirac
12 Derivada de la función delta
(función doble impulso)
13 Teorema del valor inicial
14 Teorema del valor final
REVISIÓN 5 – 75636.04
L  
n
n
n
n
t
 as
dn
F s
ds n
L  ddt f   s F  s   s
8
at
 as

Transformada de integral
 F  s  a
L  f t  aU t  a  e L  f t   e F  s 
L e F  s   L F  s  U t  a  f t  aU t  a
at
L  ddt f   s F  s   sf 
7
s  s a
s  s a
 F s
f t  dt  
s

  f  
f
  s n
f 
    sf n     f n   
L  f * g  L  f t L g t   F  s G  s 
L F  s G  s   f * g

L  f t  
e
 sT
L g t  
e
 sT
L  t  t   e


 st
T
e  st f t  dt
T
e  st g t  dt
donde
L  dtd
t  t    se  st
t
s 
t 
s

 , t  t
 , t t
t  t   
lim f t   lim  sF  s 
lim f t   lim  sF  s 
Página 2 de 2