Víctor Benites - prof.usb.ve.
Anuncio

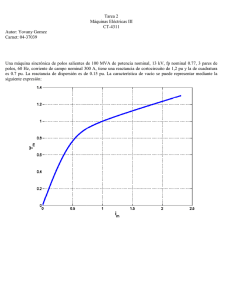
Universidad Simón Bolívar Conversión de Energía Eléctrica IV CT-4311 Víctor Benites Carnet: 07-40648 TAREA 2 1. Calcule la máxima potencia reactiva que puede entregar la máquina como condensador sincrónico Para calcular la potencia reactiva máxima como condensador sincrónico primero se debe calcular la corriente de campo máxima. Tomamos el punto nominal porque en ese punto la corriente de campo es máxima. Calculo Ie, Ee, D, Eq 1 ∗ 31.19 1.0143 ∗ 1.4116 ∗ cos 9.65 21.18 1.0921 Con Eq nos vamos a la característica lineal y sacamos el Ifl como la característica lineal tiene pendiente 2 la relación queda: 0.5461 2 Luego para Ifs evaluamos el valor de Eq en la función de saturación. 1.3723 Con esto calculamos el grado de saturación s, con s calculamos Xds y Id para calcular el Efs 2.513 1 ∗ 0.5184 ∗ sin 0.7985 ∗ 1.3464 Ahora calculamos la Ifmax con ml es la pendiente de la zona lineal ∗ 1.692 % Algoritmo para calcular Ifmax ve=1; fpn=0.85; xd=1; xq=0.6; xdis=0.2;pn=0.85;qn=0.527;m=2; ie=(pn-1i*qn)/ve; ee=ve+1i*xdis*ie; d=ve+1i*xq*ie; eq=abs(ee)*cos(angle(d)-angle(ee)); ifl=eq/2; Psim =abs(eq); ifs=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; s=ifs/ifl; xds=xd/s+(s-1)/s*xdis; id=abs(ie)*sin(angle(d)-angle(ie)); efs=abs(d)+(xds-xq)*id; ifmax=s*efs/m; .5 Zona saturacion Zona lineal Efs X: 0.682 Y: 1.346 X: 1.701 Y: 1.346 Eq X: 0.552 Y: 1.092 1 X: 1.377 Y: 1.092 .5 0 0 0.5 1 1.5 i 2 2.5 Ahora calculamos la Qmax como condensador sincrónico empezamos asumiendo que la corriente de campo en máxima y que el deslizamiento en el nominal y que el angulo de carga es 0 Usando el Xds del punto anterior calculamos la Q 1 0.6682 0.6682 ∗ 1.1336 1.1336 0.5668 2 Evaluando en la función Ifs=1.5507 2.7359 ∗ 1.3464 Sacamos el promedio para iterar 1 2 2 2.6244 Tabla de las iteraciones para una diferencia de 0.01 del grado de saturacion Q s tolerancia 0.6861 0.5813 0.5158 0.5320 0.5749 0.5914 0.5782 2.7548 2.6433 2.5728 2.5902 2.6364 2.6542 2.64 0.2229 0.1304 0.0759 0.0441 0.0256 0.0148 0.008 Aquí podemos ver que la Q se estabiliza en 0.5782 Qsinc=0.5782 %Algoritmo para calcula la Qsinc 1 2 2 2.6896 2.6665 2.6196 2.6049 2.6207 2.6374 2.6387 while(abs(res)>0.01) xds=xd/s+((s-1)/s)*xdis; Q=(efs-1)/xds; ie=Q; Ee=ve+xdis*ie; Eq=abs(Ee); ifl=abs(Eq)/2; tauT = fT / PsiT * Lm0/Lmsat; Psim =abs(Eq); Mf=1/Lmsat; Mi=(1/Lm0- 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); ifs=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; sn=ifs/ifl; efs=2*ifmax/s; res=s-sn; s=(sn+s)/2; end Qsincronica=Q; display(Qsincronica) 2. La corriente de campo máxima La corriente max es la encontrada en el punto anterior igual a 1.6917 Multiplicando por la ifn nos que da 169.17 3. La corriente de campo mínima para potencia activa nominal Para calcular la corriente de campo minina para la potencia activa nominal, fijo un valor de Ef, calculo el grado de saturación con esto grafico la P verifico si la Pn corta a la curva en su pico si no es asi cambio el valor de Ef y repito el procedimiento % Algoritmo para calcular las curvas de P res=2; x=0:0.001:pi; n=length(x); P=zeros(n,1); Q=zeros(n,1); Ef=0.4:0.015:0.7; figure hold on k=0; for a=1:length(Ef) ef = Ef(a); while(abs(res)>0.001) k=k+1; xds=xd/s+(s-1)/s*xdis; Q(k)=(ve*ef)/xds*cos(x(k))(ve^2)*((cos(x(k))^2)/xds+((sin(x(k))^2)/xq)); P(k)=ve*ef/xds*sin(x(k))+0.5*ve*ve*sin(2*x(k))*((1/xq)(1/xds)); ie=(P(k)-1i*Q(k))/ve; d=ve+xq*1i*ie; Ee=ve+xdis*1i*ie; Eq=abs(Ee)*cos(angle(d)-angle(Ee)); ifl=abs(Eq)/2; tauT = fT / PsiT * Lm0/Lmsat; Psim =abs(Eq); Mf=1/Lmsat; Mi=(1/Lm0 - 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); ifs=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; sn=ifs/ifl; res=s-sn; s=sn; end xds=xd/s+(s-1)/s*xdis; P=ve*ef/xds*sin(x)+0.5*ve*ve*sin(2*x)*((1/xq)-(1/xds)); plot(x*180/pi,P); end grid a=0:0.1:180; Pn=0.85*ones(length(a),1); plot(a,Pn,'--k') %De la grafica vemos que la curva que corta en su punto maximo %es en Ef=0.59647; angulo de carga=70.2; figure hold on efmin=0.59647; while(abs(res)>0.001) k=k+1; xds=xd/s+(s-1)/s*xdis; Q(k)=(ve*ef)/xds*cos(x(k))(ve^2)*((cos(x(k))^2)/xds+((sin(x(k))^2)/xq)); P(k)=ve*ef/xds*sin(x(k))+0.5*ve*ve*sin(2*x(k))*((1/xq)(1/xds)); ie=(P(k)-1i*Q(k))/ve; d=ve+xq*1i*ie; Ee=ve+xdis*1i*ie; Eq=abs(Ee)*cos(angle(d)-angle(Ee)); ifl=abs(Eq)/2; tauT = fT / PsiT * Lm0/Lmsat; Psim =abs(Eq); Mf=1/Lmsat; Mi=(1/Lm0 - 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); ifs=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; sn=ifs/ifl; res=s-sn; s=sn; end xds=xd/s+(s-1)/s*xdis; Pefmin=ve*efmin/xds*sin(x)+0.5*ve*ve*sin(2*x)*((1/xq)(1/xds)); plot(x*180/pi,Pefmin) plot(a,Pn,'--k') grid efmin=0.5965 ifmin=0.4262 ifmin=42.62A Curvas de P para distintos valores de Ef 1 0.9 Pn 0.8 0.7 P en pu 0.6 0.5 0.4 0.3 0.2 0.1 0 0 20 40 60 80 angulo de carga 100 120 140 160 180 P para Ef =0.59647 0.9 0.8 0.7 0.6 P en pu 0.5 0.4 0.3 0.2 0.1 0 0 20 40 60 80 angulo de carga 100 120 140 160 180 4. El punto de operación a potencia nominal y factor de potencia unitario Para este punto tenemos la P y el factor de Potencia por ende aplicamos el método directo 0.85 ∗ D Ve 1.0143 jXq ∗ Ie 1.1225 ∗ cos 27.02 0 9.648 27.02 0.9681 0.484 2 0.8956 1.8502 1 ∗ 0.7598 ∗ cos 0.3864 ∗ ∗ 1.2502 1.1565 115.65 % Algoritmo Pregunta CUATRO p=pn; q=0; fp=1; ie=(p-1i*q)/ve; ee=ve+1i*xdis*ie; d=ve+1i*xq*ie; eq=abs(ee)*cos(angle(d)-angle(ee)); ifl44=eq/2; Psim =abs(eq); ifs44=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; s44=ifs44/ifl44; xds44=xd/s+(s-1)/s*xdis; id44=abs(ie)*sin(angle(d)-angle(ie)); efs44=abs(d)+(xds44-xq)*id; ifop44=s44*efs44/m; 5. El punto de operación a potencia de 30 MW y corriente de campo máxima Como solo nos dan potencia y corriente de campo hacemos el método inverso asumiendo un s inicial igual al del punto nominal y corriente de campo igual a 1.6917 pu Pop = 0.6 Ifmax = 1.6917 ∗ 1.339 Empezamos iteración con s=2.64, calculamos primero el Xds 1 ∗ 0.503 Ahora calculamos el Angulo de carga con la ecuación de P ∗ 1 ∗ 2 ∗ sin ∗ sin 2 ∗ 1 1 15.46 Sustituyendo y resolviendo la ecuación nos queda Ahora sustituimos en la ecuación de Q y calculamos ∗ ∗ cos ∗ cos sin 0.5024 Tenemos P y Q podemos hacer el método directo para hayar un s que este más cerca del s de operación 0.7826 ∗ D Ve 39.94 1.107 6.22 jXq ∗ Ie 1.35 15.46 ∗ cos 27.02 0 1.0927 2 0.5463 1.3744 1 2.5157 Sacamos el promedio entre los primeros números para realizar menos iteraciones 1 2 ∗ 2.5778 1.3189 Tabla con las iteraciones iteración 2 3 15.11 15.10 Q 0.5555 0.5558 Eq 1.1040 1.1045 s 2.5771 2.5774 (s1+s2)/2 2.5775 2.5776 Efs 1.3191 1.3191 %Pregunta CINCO p5=0.6; s=2.64; res=1; efs=3.4/s; efs5=3.4; while(abs(res)>0.0001) xds=xd/s+(s-1)/s*xdis; display(xds) x = 0:0.0001:pi; k = 0; Pcalc = 0; while (abs(Pcalc-p5)>0.0001) k = k+1; Pcalc=ve*efs/xds*sin(x(k))+0.5*ve*ve*sin(2*x(k))*((1/xq)(1/xds)); end display(x(k)*180/pi) Q=(ve*efs)/xds*cos(x(k))(ve^2)*((cos(x(k))^2)/xds+((sin(x(k))^2)/xq)); display(Q) ie=(p5-1i*Q)/ve; display(abs(ie)) display(angle(ie)*180/pi) d=ve+xq*1i*ie; display(d) Ee=ve+xdis*1i*ie; display(Ee) Eq=abs(Ee)*cos(angle(d)-angle(Ee)); display(Eq) ifl=abs(Eq)/2; display(ifl) tauT = fT / PsiT * Lm0/Lmsat; Psim =abs(Eq); Mf = 1/Lmsat; Mi = (1/Lm0 - 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) - PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; display(ifs) sn=ifs/ifl; display(sn) res=s-sn; s=(sn+s)/2; display(s) efs=efs5/s; display(efs) end s5=s; display(s5) x5=x(k); display(x5*180/pi) 6. El punto de operación a potencia de -40 MW y corriente de campo nominal Como solo nos dan potencia y corriente de campo hacemos el método inverso asumiendo un s inicial igual al del punto nominal y corriente de campo igual a 1 pu ∗ 0.7813 Empezamos iteración con s=2.64, calculamos primero el Xds 1 ∗ 0.503 Ahora calculamos el Angulo de carga con la ecuación de P ∗ ∗ sin 1 ∗ 2 ∗ sin 2 Sustituyendo y resolviendo la ecuación nos queda ∗ 1 1 17.65 Ahora sustituimos en la ecuación de Q y calculamos ∗ ∗ cos ∗ cos sin 0.8442 Tenemos P y Q podemos hacer el método directo para hayar un s que este más cerca del s de operación 1.163 ∗ D Ve 133.46 1.180 jXq ∗ Ie 7.78 1.581 ∗ cos 27.02 17.67 0 1.1622 0.5811 2 1.6767 1 2.8853 Sacamos el promedio entre los primeros números para realizar menos iteraciones 1 2 ∗ iteración 2 3 4 -27.87 -26.1652 -26.1773 Q -0.154 -0.0384 -0.0392 Eq 0.9316 0.9612 0.961 1.9426 1.0295 s 1.6889 1.8176 1.8166 %Pregunta SEIS function F = myfun(x) global xq1 p6 xds1 efs1 F=(((efs1)/xds1)*sin(x))+(1/2)*((((1/xq1)(1/xds1))*sin(2*x)))-p6; end s=1; global xq1 p6 xds1 efs1 efs1=2/s; display(s) p6=-0.8; xq1=0.6; efs6=2; res=1; while(abs(res)>0.001) xds1=xd/s+(s-1)/s*xdis; x0=0; [x,fval] = fsolve(@myfun,x0); (s1+s2)/2 1.8158 1.8167 1.8167 efs 1.1015 1.1009 1.1009 display(x*180/pi) Q=(ve*efs1)/xds1*cos(x)(ve^2)*((cos(x)^2)/xds1+((sin(x)^2)/xq1)); display(Q) ie=(p6-1i*Q)/ve; angleie=angle(ie); modie=abs(ie); display(angleie*180/pi) display(modie) d=ve+xq1*1i*ie; display(d) Ee=ve+xdis*1i*ie; display(Ee) Eq=abs(Ee)*cos(angle(d)-angle(Ee)); display(Eq) ifl=abs(Eq)/2; tauT = fT / PsiT * Lm0/Lmsat; Psim =abs(Eq); Mf = 1/Lmsat; Mi = (1/Lm0 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi ) ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(PsimPsiT)) - PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) - log(1+tauT^2*(PsimPsiT).^2)) ) + Psim.*(Mf+Mi)/2; sn=ifs/ifl; display(ifl) display(ifs) res=s-sn; display(sn) s=(sn+s)/2; display(s) efs1=efs6/s; display(efs1) end display(efs1) display(s) angleie=angle(ie)*180/pi; display(angleie) 7. Suponiendo que desconoce las reactancias Xd y Xq, determine estos parámetros utilizando el punto nominal y los resultados de la primera pregunta (Asuma conocida la reactancia de dispersión) Para calcular la Xd tomamos los datos de la pregunta del condensador sincrónico y la corriente máxima como conocidos. Luego tomamos el ángulo de carga como cero por la condición y calculamos el s para ese punto con esto vario la Xd hasta que la Q que calcule sea igual a la Q como condensador sincronica %Pregunta SIETE Q7=0.5781; If=ifmax; x=0; efs=If*2/s; ie=Q7; Ee=ve+xdis*ie; Eq=abs(Ee); ifl=abs(Eq)/2; tauT = fT / PsiT * Lm0/Lmsat; Psim =abs(Eq); Mf=1/Lmsat; Mi=(1/Lm0- 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); ifs=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; sn=ifs/ifl; display(sn) xd7=0:0.00001:2; n=length(xd7); Q7=0.5782; for a=1:length(xd7) Q=0.2879/((0.3788*xd7(a)+0.1242)); if abs(Q-Q7)<0.00585 xdn=xd7(a); end end display(xdn) Al corer el algoritmo nos da Xd=1.000 igual al valor que es dato Ahora para calcular Xq usamos el punto nominal como sabemos p y q usamos el método directo, calculamos la corriente para un Xq el cual asumimos si con ese Xq la corriente es igual la Ifmax entonces ese Xq es el valor que buscamos pero si el If que nos da es menos aumentamos Xq y si es mayor disminuimos el Xq hasta que el if que calculemos sea igual al ifmax xq7=0.1:0.000001:2; k=0; res = 1; p=0.85;q=0.5268; ie=(p-1i*q)/ve; while(abs(res)>0.00001) k = k+1; ee=ve+1i*xdis*ie; d=ve+xq7(k)*1i*ie; eq=abs(ee)*cos(angle(d)-angle(ee)); ifl=abs(eq)/2; tauT=fT/PsiT*Lm0/Lmsat; Psim =abs(eq); Mf=1/Lmsat; Mi=(1/Lm0- 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); ifs=(Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(PsimPsiT)) - PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) - log(1+tauT^2*(PsimPsiT).^2)) ) + Psim.*(Mf+Mi)/2; sn=ifs/ifl; xds=(xd/sn)+(sn-1)*xdis/sn; id=abs(ie)*sin(angle(d)-angle(ie)); efs=abs(d)+(xds-xq7(k))*id; ifmax1=efs*sn/m; res=ifmax1-ifmax; end display(xq7(k)) al finalizar el programa la Xq da 0.5992 muy cercana a los 0.6 que eran dato 8. Suponiendo que desconoce las reactancias Xd y Xq, determine estos parámetros utilizando los resultados obtenidos en las pregunas 5 y 6 (Asuma conocida la reactancia de dispersión) Aquí tenemos cuatro ecuaciones con cuatro incógnitas para calcularla asumimos un valor de Xd con esto aplicamos el método directo variando Xq hasta que el valor de if5 que calculamos de igual al if del pregunta 5, con estos Xq y Xd calculamos con el método directo el valor de if6 si este valor es igual al if de la pregunta 6 entonces esos Xq y Xd son los que buscamos porque cumplen con los dos puntos en caso contrario aumentamos el valor de Xd y repetimos el procedimiento hasta que converge . % CARACTERISTICA DE VACIO Lm0= 2; % Inductancia no saturada Lmsat= .2; % Inductancia saturada PsiT= .93; % Flujo de transición fT= 1; % Anchura de la transición iT = 1/Lm0*PsiT; Psimax = 4*iT*Lmsat+PsiT; Psim = (0:0.00001:1)*Psimax; tauT = fT / PsiT * Lm0/Lmsat; Mf = 1/Lmsat; Mi = (1/Lm0 - 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi); im = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2; % ajuste zona lineal % Efl = ifl*ml ml = 2; % Reactancia de dispersion Xdisp = 0.2; % PREG5: P=30MW y ifmax Ve5 = 1; P5 = 30/50; Q5 = 0.54912; S5 = sqrt(P5^2+Q5^2); fp5 = P5/S5; if5 = 1.6914; Ie5 = (P5-1i*Q5)/Ve5; % PREG6: P=-40 MW y ifnom Ve6 = 1; P6 = -40/50; Q6 = -0.039181; S6 = sqrt(P6^2+Q6^2); fp6 = P6/S6; if6 = 1; Ie6 = (P6-1i*Q6)/Ve6; Xdd = 0.8:0.001:1.1; Ee5 = Ve5 + 1i*Xdisp*Ie5; Ee6 = Ve6 + 1i*Xdisp*Ie6; ifmax6 = 0; ifmax5 = 0; Xd = 0.97; Xq5 = 0.57; while(abs(ifmax6-if6)>0.001) Xd = Xd +0.01; ifmax5 = 0; Xq5 = 0.6; while(abs(ifmax5-if5)>0.01) Xq5 = Xq5+0.001; D5 = Ve5 + 1i*Xq5*Ie5; Eq5 = abs(Ee5)*cos(angle(D5)-angle(Ee5)); ifl5 = abs(Eq5)/ml; Psim = abs(Eq5); ifs5 = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(PsimPsiT)) - PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) - log(1+tauT^2*(PsimPsiT).^2)) ) + Psim.*(Mf+Mi)/2; ss5 = ifs5/ifl5; Xds5 = Xd/ss5+(ss5-1)/ss5*Xdisp; Id5 = abs(Ie5)*sin(angle(D5)-angle(Ie5)); Efmax5 = abs(D5)+(Xds5-Xq5)*Id5; ifmax5 = ss5*Efmax5/ml; end Xq6 = Xq5; D6 = Ve6 + 1i*Xq6*Ie6; Eq6 = abs(Ee6)*cos(angle(D6)-angle(Ee6)); ifl6 = abs(Eq6)/ml; Psim = abs(Eq6); ifs6 = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(PsimPsiT)) - PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) - log(1+tauT^2*(PsimPsiT).^2)) ) + Psim.*(Mf+Mi)/2; ss6 = ifs6/ifl6; Xds6 = Xd/ss6+(ss6-1)/ss6*Xdisp; Id6 = abs(Ie6)*sin(angle(D6)-angle(Ie6)); Efmax6 = abs(D6)+abs((Xds6-Xq6)*Id6); ifmax6 = ss6*Efmax6/ml; end display(Xd) display(Xq5) Al ejecutar el algoritmo nos da una Xq=1 con respecto al Xq= 1 es totalmente idéntico y Xd da 0.6010 que con respecto a los 0.6 que debería dar el error es insignificante