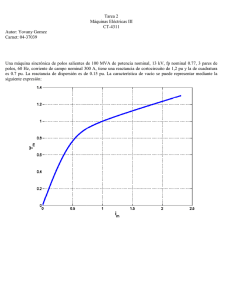
Una máquina sincrónica de rotor liso de 100 MVA de potencia
Anuncio

Universidad Simón Bolívar
Departamento de Conversión y Transporte de Energía
Conversión de Energía III
Profesor: José Manuel Aller
Alumno: Anthony Bujosa
TAREA #2
Una máquina sincrónica de rotor liso de 100 MVA de potencia nominal, 10 kV, fp nominal
0.85, un par de polos, 60 Hz, corriente de campo nominal 300 A, tiene una reactancia de
cortocircuito de 1,0 pu. La reactancia de dispersión es de 0.2 pu. La característica de vacío
se puede representar mediante la siguiente función en Matlab:
%
%
%
%
Lm0:
Lmsat:
PsiT:
fT:
Inductancia no saturada
Inductancia saturada
Flujo de transición
Anchura de la transición
(2
(.2
(.93
(1
pu)
pu)
pu)
pu)
function plsaturation(Lm0, Lmsat, PsiT, fT)
iT = 1/Lm0*PsiT;
Psimax = 4*iT*Lmsat+PsiT
Psim = [0:0.002:1]*Psimax;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
im = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
plot(im,Psim);
ylabel('\Psi_m');
xlabel('i_m');
grid on;
1. Calcule la máxima potencia reactiva que puede entregar la máquina como
condensador sincrónico
2. La corriente de campo máxima
3. La corriente de campo mínima para potencia activa nominal
4. El punto de operación a potencia nominal y factor de potencia unitario
5. El punto de operación a potencia de 30 MW y corriente de campo máxima
6. El punto de operación a potencia de -40 MW y corriente de campo nominal
7. La característica de potencia activa en función del ángulo de carga
8. El lugar geomético de la corriente de armadura que no viola límites de operación.
9. Determine el triángulo de Potier de esta máquina
10. Determine las curvas en V a tensión nominal para P=[0, 0.2, 0.4, 0.6, 0.8 y 1.0} pu
1.
Calcule la máxima potencia reactiva que puede entregar la máquina como
condensador sincrónico
1.4
1.2
1
m
0.8
0.6
0.4
0.2
0
Curva de vacío
Linealización
0
0.5
1
1.5
2
2.5
im
Figura1.1. Curva de vacío de la Máquina y su linealización.
De los datos del punto nominal se puede obtener la corriente máxima de campo sabiendo
que ésta viene determinada por el factor de potencia nominal
Se tiene que la máquina sincrónica de rotor liso se puede trabajar como una de polos
salientes considerando el fenómeno de saturación en ambos ejes (cuadratura y directo)
Inicialmente se supone el grado de saturación unitario en el eje cuadratura
Se puede apreciar que Ed se encuentra en la zona lineal, razón por la cual no es necesario
iterar
Como se encuentra en la zona no lineal:
Donde
Finalmente se tiene la corriente de campo máxima
Para obtener la máxima potencia reactiva como compensador sincrónico se plantea un caso
inverso donde
:
Y aplicando un proceso iterativo de la Rutina 1:
2. Corriente de campo máxima
Del punto anterior se tiene
3.
La corriente de campo mínima para potencia activa nominal
Potencia vs angulo de carga
2
Potencia (p.u)
1.5
Pn=0.85
1
0.5
0
0
20
40
60
80
100
120
Angulo de carga (°)
140
160
180
Figura3.1. Potencia eléctrica en función del ángulo para distintos valores de corriente de campo.
De acuerdo a la Rutina 2:
4. El punto de operación a potencia nominal y factor de potencia unitario
Eje q
Ef
J(Xds-Xqs).Id
jXqs.Ie
Eq
D
δ
Ed
Jxσ.Ie
Ee
e
Ej
Ie
Ve
d
Figura 4.1. Diagrama fasorial de la máquina con factor de potencia unitario.
Se tiene un problema directo en el cual debemos iterar hasta converger en Ed suponiendo
inicialmente el grado de saturación unitario en el eje q como se muestra en la Rutina 3
Finalmente se tiene:
5. El punto de operación a potencia de 30 MW y corriente de campo máxima
Para este caso no es posible obtener directamente la corriente del estator como fasor, razón
por la cual estamos en presencia de un problema inverso el cuál se resolverá utilizando la
Rutina 4
PUNTO DE OPERACIÓN
0,3
11.4993 °
0,4747
0,5342
1
1,2675
0,3000 – 0,4734i
1,5677
2,3002
1
Tabla 5. Punto de operación para 30MW y corriente de campo máxima.
6. El punto de operación a potencia de -40 MW y corriente de campo nominal
Para este punto seguimos en presencia de un problema inverso en cuál se resolverá nuevamente
utilizando la Rutina 4, tomando la previsión de cambiar el valor de la corriente de campo y la
potencia
PUNTO DE OPERACIÓN
-0,4
-20,7239°
0,0571
-0,99
1
1,0635
-0,4000 – 0,0571i
1
1,7486
1
Tabla 6. Punto de operación para -40MW y corriente de campo nominal.
7. La característica de potencia activa en función del ángulo de carga
Potencia vs angulo de carga
3
Potencia (p.u)
2.5
2
1.5
1
Característica con saturación
Característica sin saturación
0.5
0
0
20
40
60
80
100
120
Angulo de carga (°)
140
160
Figura 6. Característica potencia vs ángulo.
Utilizando la Rutina 5 se obtiene la característica mostrada con en la Figura 6
180
1
Rutinas en utilizadas para la resolución de algunos puntos, en el entorno Matlab
RUTINA 1
function [iT,Mf,Mi,S,SS,Q]=Qmax(Lm0, Lmsat, PsiT, fT)
ifmax=1.5677; Ve=1;
m=1.8598; n=1;
iT = 1/Lm0*PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
Xdis=0.2; Xd=1;
S(n)=1;
Xds=Xdis*(S(n)-1)/S(n)+Xd/S(n);
Q(n)=(m*ifmax/S(n)-1)/Xds;
Ie=-Q(n)*1i;
Eq=Ve+Xdis*Ie*1i;
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SS(n)=ifs/ifl;
while abs(S(n)-SS(n))>0.001
n=n+1;
S(n)=(S(n-1)+SS(n-1))/2;
Xds=Xdis*(S(n)-1)/S(n)+Xd/S(n);
Q(n)=(m*ifmax/S(n)-1)/Xds;
Ie=-Q(n)*1i;
Eq=Ve+Xdis*Ie*1i;
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SS(n)=ifs/ifl;
end
end
RUTINA 2
Ve=1; Xd=1; Xq=1; Xdis=0.2; m=1.8598;
iT = 1/Lm0*PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
for ifmax=1:-0.1:0.4
n=0; nn=0;
for delta=0.001:0.01:pi;
nn=nn+1;
n=n+1;
Sd(n)=1; Sq(n)=1;
Xqs=Xdis*(Sq(n)-1)/Sq(n)+Xq/Sq(n); Xds=Xdis*(Sd(n)-1)/Sd(n)+Xd/Sd(n);
P(n)=Ve*ifmax*m*sin(delta)/(Sd(n)*Xds)+Ve^2*(1/Xqs1/Xds)*sin(2*delta)/2;
Q=Ve*ifmax*m*cos(delta)/(Sd(n)*Xds)Ve^2*(cos(delta)^2/Xds+sin(delta)^2/Xqs);
Ie=P(n)-Q*1i;
Ee=Ve+Xdis*Ie*1i;
D=Ve+Xqs*Ie*1i;
Ed=abs(Ee)*sin(angle(D)-angle(Ee));
Psim=Ed;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed/m;
SSq(n)=ifs/ifl;
if SSq(n)<1
SSq(n)=1;
end
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SSd(n)=ifs/ifl;
if SSd(n)<1
SSd(n)=1;
end
while abs(Sd(n)-SSd(n))>0.001 || abs(Sq(n)-SSq(n))>0.001
n=n+1;
Sd(n)=(Sd(n-1)+SSd(n-1))/2;
Sq(n)=(Sq(n-1)+SSq(n-1))/2;
Xqs=Xdis*(Sq(n)-1)/Sq(n)+Xq/Sq(n);
Xds=Xdis*(Sd(n)-1)/Sd(n)+Xd/Sd(n);
P(n)=Ve*ifmax*m*sin(delta)/(Sd(n)*Xds)+Ve^2*(1/Xqs1/Xds)*sin(2*delta)/2;
Q=Ve*ifmax*m*cos(delta)/(Sd(n)*Xds)Ve^2*(cos(delta)^2/Xds+sin(delta)^2/Xqs);
Ie=P(n)-Q*1i;
Ee=Ve+Xdis*Ie*1i;
D=Ve+Xqs*Ie*1i;
Ed=abs(Ee)*sin(angle(D)-angle(Ee));
Psim=Ed;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed/m;
SSq(n)=ifs/ifl;
if SSq(n)<1
SSq(n)=1;
end
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SSd(n)=ifs/ifl;
if SSd(n)<1
SSd(n)=1;
end
Id=abs(Ie)*sin(angle(D)-angle(Ie));
Ef=abs(D)+(Xds-Xqs)*Id;
ifm=Ef*Sd(n)/m;
end
pot(nn)=P(n);
delt(nn)=delta*180/pi;
end
plot(delt,pot);grid minor
title('Potencia vs angulo de carga')
ylabel('Potencia (p.u)')
xlabel('Angulo de carga (°) ')
hold on
plot(delt,pot)
end
end
RUTINA 3
function [S,Sd,Ed,Xqs,Xds,D,Eq]=Rutina3(Lm0, Lmsat, PsiT, fT)
Ve=1; Ie=0.85;
iT = 1/Lm0*PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
Xdis=0.2; Xq=1; Xd=1;
n=1; m=1.8598;
S(n)=1;
Xqs=Xdis*(S(n)-1)/S(n)+Xq/S(n);
Ee=Ve+Xdis*Ie*1i;
D(n)=Ve+Xqs*Ie*1i;
Ed(n)=abs(Ee)*sin(angle(D(n))-angle(Ee));
Psim=Ed(n);
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed(n)/m;
SS(n)=ifs/ifl;
while abs(S(n)-SS(n))>0.001
n=n+1;
S(n)=(S(n-1)+SS(n-1))/2;
Xqs=Xdis*(S(n)-1)/S(n)+Xq/S(n);
Ee=Ve+Xdis*Ie*1i;
D(n)=Ve+Xqs*Ie*1i;
Ed(n)=abs(Ee)*sin(angle(D(n))-angle(Ee));
Psim=Ed(n);
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed(n)/m;
SS(n)=ifs/ifl;
end
Eq=abs(Ee)*cos(angle(D(n))-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
Sd=ifs/ifl;
Xds=Xdis*(Sd-1)/Sd+Xd/Sd;
Id=abs(Ie)*sin(angle(D(n)))
Ef=abs(D(n))+(Xds-Xqs)*Id
end
RUTINA 4
function [x,Sd,SSd,Q,SSq,Xds,Xqs]=Rutina4(Lm0, Lmsat, PsiT, fT)
global Ve m Sd Sq Xds Xqs PD ifmax n
n=1;
PD=30/100; ifmax=1.5677; Ve=1; Xd=1; Xq=1; Xdis=0.2; m=1.8598;
iT = 1/Lm0*PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
Sd(n)=1; Sq(n)=1;
x0=0;
Xqs=Xdis*(Sq(n)-1)/Sq(n)+Xq/Sq(n); Xds=Xdis*(Sd(n)-1)/Sd(n)+Xd/Sd(n);
x=fsolve(@Pfun,x0);
Q=Ve*ifmax*m*cos(x)/(Sd(n)*Xds)-Ve^2*(cos(x)^2/Xds+sin(x)^2/Xqs);
Ie=PD-Q*1i;
Ee=Ve+Xdis*Ie*1i;
D=Ve+Xqs*Ie*1i;
Ed=abs(Ee)*sin(angle(D)-angle(Ee));
Psim=Ed;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed/m;
SSq(n)=ifs/ifl;
if SSq(n)<1
SSq(n)=1;
end
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SSd(n)=ifs/ifl;
if SSd(n)<1
SSd(n)=1;
end
while abs(Sd(n)-SSd(n))>0.001 ||abs(Sq(n)-SSq(n))>0.001
n=n+1;
Sd(n)=(Sd(n-1)+SSd(n-1))/2;
Sq(n)=(Sq(n-1)+SSq(n-1))/2;
Xqs=Xdis*(Sq(n)-1)/Sq(n)+Xq/Sq(n)
Xds=Xdis*(Sd(n)-1)/Sd(n)+Xd/Sd(n)
x=fsolve(@Pfun,x0);
Q=Ve*ifmax*m*cos(x)/(Sd(n)*Xds)-Ve^2*(cos(x)^2/Xds+sin(x)^2/Xqs);
Ie=PD-Q*1i;
Ee=Ve+Xdis*Ie*1i;
D=Ve+Xqs*Ie*1i;
Ed=abs(Ee)*sin(angle(D)-angle(Ee));
Psim=Ed;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed/m;
SSq(n)=ifs/ifl;
if SSq(n)<1
SSq(n)=1;
end
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SSd(n)=ifs/ifl;
if SSd(n)<1
SSd(n)=1;
end
Id=abs(Ie)*sin(angle(D)-angle(Ie));
Ef=abs(D)+(Xds-Xqs)*Id;
ifm=Ef*Sd(n)/m;
end
%FUNCIÓN PARA EL fsolve
function P=Pfun(delta)
global Ve m Sd Xds Xqs PD ifmax n
P=Ve*m*ifmax*sin(delta)/(Sd(n)*Xds)+Ve^2*(1/Xqs-1/Xds)*sin(2*delta)/2-PD;
end
RUTINA 5
function [pot,Sd,SSd,delta,SSq,Xds,Xqs]=Rutina5(Lm0, Lmsat, PsiT, fT)
n=0; nn=0;
ifmax=1.5677; Ve=1; Xd=1; Xq=1; Xdis=0.2; m=1.8598;
iT = 1/Lm0*PsiT;
tauT = fT / PsiT * Lm0/Lmsat;
Mf = 1/Lmsat;
Mi = (1/Lm0 - 1/Lmsat*(.5-atan(tauT*PsiT)/pi))/(.5+atan(tauT*PsiT)/pi);
for delta=0.001:0.01:pi;
nn=nn+1;
n=n+1;
Sd(n)=1; Sq(n)=1;
Xqs=Xdis*(Sq(n)-1)/Sq(n)+Xq/Sq(n); Xds=Xdis*(Sd(n)-1)/Sd(n)+Xd/Sd(n);
P(n)=Ve*m*ifmax*sin(delta)/(Sd(n)*Xds)+Ve^2*(1/Xqs1/Xds)*sin(2*delta)/2;
Q=Ve*ifmax*m*cos(delta)/(Sd(n)*Xds)Ve^2*(cos(delta)^2/Xds+sin(delta)^2/Xqs);
Ie=P(n)-Q*1i;
Ee=Ve+Xdis*Ie*1i;
D=Ve+Xqs*Ie*1i;
Ed=abs(Ee)*sin(angle(D)-angle(Ee));
Psim=Ed;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed/m;
SSq(n)=ifs/ifl;
if SSq(n)<1
SSq(n)=1;
end
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SSd(n)=ifs/ifl;
if SSd(n)<1
SSd(n)=1;
end
while abs(Sd(n)-SSd(n))>0.001 || abs(Sq(n)-SSq(n))>0.001
n=n+1;
Sd(n)=(Sd(n-1)+SSd(n-1))/2;
Sq(n)=(Sq(n-1)+SSq(n-1))/2;
Xqs=Xdis*(Sq(n)-1)/Sq(n)+Xq/Sq(n);
Xds=Xdis*(Sd(n)-1)/Sd(n)+Xd/Sd(n);
P(n)=Ve*m*ifmax*sin(delta)/(Sd(n)*Xds)+Ve^2*(1/Xqs1/Xds)*sin(2*delta)/2;
|
Q=Ve*ifmax*m*cos(delta)/(Sd(n)*Xds)Ve^2*(cos(delta)^2/Xds+sin(delta)^2/Xqs);
Ie=P(n)-Q*1i;
Ee=Ve+Xdis*Ie*1i;
D=Ve+Xqs*Ie*1i;
Ed=abs(Ee)*sin(angle(D)-angle(Ee));
Psim=Ed;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Ed/m;
SSq(n)=ifs/ifl;
if SSq(n)<1
SSq(n)=1;
end
Eq=abs(Ee)*cos(angle(D)-angle(Ee));
Psim=Eq;
ifs = (Mf-Mi)/pi*(((Psim-PsiT).*atan(tauT*(Psim-PsiT)) PsiT*atan(tauT*PsiT))+ .5/tauT*(log(1+(tauT*PsiT)^2) log(1+tauT^2*(Psim-PsiT).^2)) ) + Psim.*(Mf+Mi)/2;
ifl=Eq/m;
SSd(n)=ifs/ifl;
if SSd(n)<1
SSd(n)=1;
end
Id=abs(Ie)*sin(angle(D)-angle(Ie));
Ef=abs(D)+(Xds-Xqs)*Id;
ifm=Ef*Sd(n)/m;
end
pot(nn)=P(n);
delt(nn)=delta*180/pi;
end
plot(delt,pot);grid minor
title('Potencia vs angulo de carga')
ylabel('Potencia (p.u)')
xlabel('Angulo de carga (°) ')
hold on
g=0;
for delta=0:0.01:pi
g=g+1;
PP(g)=Ve*m*ifmax*sin(delta)/(Xd)+Ve^2*(1/Xq-1/Xd)*sin(2*delta)/2;
delt(g)=delta*180/pi;
end
plot(delt,PP)
end