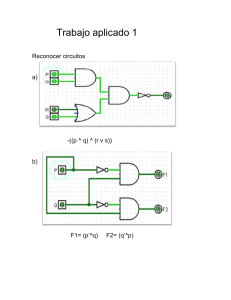
taller de logica

1. Realice la tabla de verdad de las siguientes expresiones, indicando si es una contradicción
o una tautología
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
p∧q
(p ∧ q) ∧ r
¬(p → ¬q) ∧ (p ∧ ¬q)
(p ∧ q) ∨ (p ∨ ¬q)
p∧q∧r
¬(p ∧ ¬q) ∧ (p ∧ ¬q)
¬¬(¬p ∧ ¬q) ∨ (p ∧ ¬q)
p∨q∧r
¬(¬p ∧ ¬q) ∧ (¬p ∧ ¬q)
p ∨ q ∧ ¬r
2. Si p es V y q es F, determínese el valor de verdad de las siguientes fórmulas:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
¬p → q.
¬p v ¬p
¬¬p v ¬¬q
¬q → ¬p
p →¬(p v¬q)
p v q →q
¬(¬q→p) v (¬p →q)
(¬p v ¬q) ↔ (¬p v ¬q → p)
(p → q) v ¬q → ¬p
¬¬¬p → ¬p
3. Complete las siguientes frases:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Si “p v q” es V y p es F, entonces “q” es ...
Si “¬q ∧ q” es V, entonces “p” es ...
Si “¬p ∧ ¬q” es F y “p” es F, entonces “q” es ...
Si “¬ (¬p v ¬q)” es V, entonces “p” es ...
Si “p v ¬q” es F, entonces “q” es ...
Si “p → q” es V y “p” es V, entonces “q” es ...
Si “p → q” es V y “¬q” es V, entonces “¬p” es ...
Si “p ↔ q” es F y “p” es V, entonces “q” es ...
Si “¬q → ¬p” es V y “q” es F, entonces “p” es ...
Si “p ∧ ¬q” es V, entonces “p → q” es ....