1. Deformacion en vigas - U
Anuncio

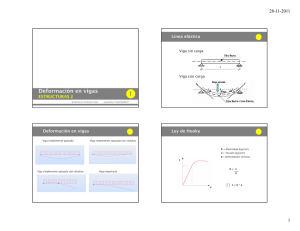
05-08-2010 Deformación en vigas 1 ESTRUCTURAS 2 profesora: Verónica Veas ayudante: Preeti Bellani Línea elástica Viga sin carga Viga con carga 1 05-08-2010 Deformación en vigas Viga simplemente apoyada Viga simplemente apoyada con voladizo Viga simplemente apoyada con voladizo Viga simplemente apoyada con voladizo Viga empotrada Ley de Hooke E = Elasticidad (kg/cm2) τ = Tensión (kg/cm2) ε = Deformación Unitaria τ E= τ ε ε 1 τ=E*ε 2 05-08-2010 Deducción fórmula de flexión τ= M W W= I V 2 τ = MV I τ = Tensión (kg/cm2) M = Momento flector (kgcm) V = Distancia desde la fibra neutra a I Igualando expresiones 1 y la fibra más traccionada o más comprimida (cm) = Inercia (cm4) 2 τ = Eεε = MV ó ε = MV I EI 3 Análisis de la sección Por relación de triángulos semejantes 0 n n’ y 4 n’ t’ t’’ ∆ds = V = ε ds R ds = dφ φ* R /:R :ds 1 = dφ φ R ds 3 05-08-2010 Igualando 3 y 4 ε = V = MV R EI /:V 1=M R EI 1 = M = dφ φ R EI ds dφ φ = M*ds EI Si ds ≈ dx La curvatura de la línea elástica es una variable proporcional al momento flector. dφ φ = Mdx EI 4 05-08-2010 Métodos de cálculo a Método de área de momentos. b Método de doble integración. c Método de la viga conjugada. Se busca determinar el ángulo de curvatura de la línea elástica y sus deflecciones o flechas. Cada método tiene ventajas y desventajas dependiendo de la viga a analizar. Estableciendo relaciones entre ángulos 5 05-08-2010 Método de doble integración dφ = M.dx EI .../ dx EI dφ M = dx EI Ecuación elástica Si... dy = tgφ dx d2 y =M dx 2 diferencial de la Integrando... tgφ ≈ φ EI dy =φ dx dy = M dx dx ∫ Ecuación general de Pendiente Reemplazando... d dy dx dx = M Integrando... d2 y M = dx 2 EI EI EI y = ∫∫ M dx Ecuación general de Flecha Ejemplo Viga simplemente apoyada con carga uniformemente repartida 1. Equilibrio externo: cálculo de reacciones qL Ra = Rb = 2 2. Determinar ecuación general de momento Mx= qLx qx2 − 2 2 6 05-08-2010 3. Definir la ecuación diferencial de la elástica. EI 2 2 d y qLx qx = MX = − 2 2 2 dx 4. Definir la ecuación general de la pendiente EI dy dx = 2 qLx 4 − 3 qx 6 + C1 5. Definir la ecuación general de la flecha EI y = qLx 3 qx 4 qL3 x + C 1 x + C2 − − 12 24 24 6. Despejar las constantes de integración Para despejar C1 ... L x= 2 dy =0 dx 2 3 qL L qL EI. 0 = − + C1 4 2 62 C1 = − EI qL3 24 dy qLx 2 qx 3 qL3 = − − dx 4EI 6EI 24EI Para despejar C2 ... y=0 x=0 x=L EI. 0 = qL 3 q 4 qL3 0 − 0 − 0 + C2 12 24 24 EI. 0 = qL 3 q 4 qL3 L − L − L + C2 12 24 24 C2 = 0 EI y = qLx 3 qx 4 qL3 x − − 12EI 24EI 24EI 7 05-08-2010 7. Determinar valores característicos. Ángulos en los apoyos... EI dy qLx 2 qx 3 qL3 = − − dx 4EI 6EI 24EI x =L x=0 3 φA = dy qL =− dx 24EI φB = dy qL3 qL3 qL3 = − − dx 4EI 6EI 24EI φB = dy qL3 = dx 24EI La flecha máxima... EI y = qLx 3 qx 4 qL3 x − − 12EI 24EI 24EI x = L/2 3 4 y= qL L q L qL3 L − − 12EI 2 24EI 2 24EI 2 y= 5qL4 384EI 8