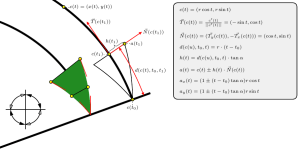
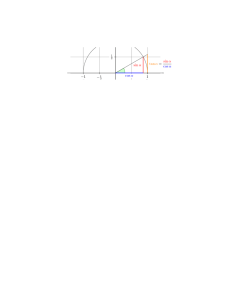
adicijski izreki
Anuncio

ADICIJSKI IZREKI tan α + tan β 1 − tan α tan β cos(α + β) = cos α cos β − sin α sin β tan α − tan β tan(α − β ) = cos(α − β ) = cos α cos β + sin α sin β 1 + tan α tan β sin(α + β) = sin α cos β + cos α sin β cot α cot β −1 cot(α + β ) = sin(α − β) = sin α cos β − cos α sin β cot α + cot β − cot α cot β −1 cot(α − β ) = cot α − cot β tan(α + β ) = PRETVARJANJE VSOTE KOTNIH FUNKCIJ V PRODUKT IN OBRATNO sin( a + b) + sin( a − b) = 2 sin a cos b x+ y x− y sin x − sin y = 2 cos sin 2 2 sin( a + b) − sin( a − b) = 2 cos a sin b x + y x − y cos(a + b) + cos(a − b) = 2 cos a cos b sin x + sin y = 2 sin cos 2 2 1 sin x cos y = (sin( x + y ) + sin( x − y )) x+ y x− y 2 cos x + cos y = 2 cos 2 cos 2 1 cos x cos y = (cos( x + y ) + cos( x − y )) x+ y x− y 2 cos x − cos y = −2 sin sin 2 2 1 sin x sin y = − (cos( x + y ) − cos( x − y )) sin(α + β ) 2 tan α + tan β = cos α cos β DVOJNI KOTI sin 2α = 2 sin α cos α cos 2α = cos 2 α − sin 2 α sin x = ± 1 − cos x 2 2 cos x = ± 1 + cos x 2 2 2 tan α tan 2α = 1 − tan 2 α cot 2 α − 1 cot 2α = 2 cot α KROŽNE FUNKCIJE 1 cos 2 x 1 1 + cot 2 x = sin 2 x π sin α = cos( − α ) 2 π cos α = sin( − α ) 2 2 2 sin α + cos α = 1 1 + tan 2 x =