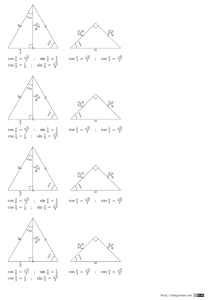
f(x) F(x) a a·x + k xn 1 n + 1 ·xn+1 + k Pour x>0, 1 x ln x
Anuncio

f (x)
F (x)
f (x)
F (x)
f (x)
F (x)
a
a·x + k
a
a·x + k
a
a·x + k
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
ln x + k
1
x2
−
1
+k
x
1
x2
−
1
+k
x
1
x2
−
1
√
x
√
2· x + k
1
√
x
√
2· x + k
1
√
x
√
2· x + k
ex
ex + k
ex
ex + k
ex
ex + k
sin x
− cos x + k
sin x
− cos x + k
sin x
− cos x + k
cos x
sin x + k
cos x
sin x + k
cos x
sin x + k
f (x)
F (x)
f (x)
F (x)
f (x)
F (x)
a
a·x + k
a
a·x + k
a
a·x + k
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
1
+k
x
ln x + k
1
x2
−
1
+k
x
1
x2
−
1
+k
x
1
x2
−
1
√
x
√
2· x + k
1
√
x
√
2· x + k
1
√
x
√
2· x + k
ex
ex + k
ex
ex + k
ex
ex + k
sin x
− cos x + k
sin x
− cos x + k
sin x
− cos x + k
cos x
sin x + k
cos x
sin x + k
cos x
sin x + k
f (x)
F (x)
f (x)
F (x)
f (x)
F (x)
a
a·x + k
a
a·x + k
a
a·x + k
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
1
+k
x
ln x + k
1
x2
−
1
+k
x
1
x2
−
1
+k
x
1
x2
−
1
+k
x
1
√
x
√
2· x + k
1
√
x
√
2· x + k
1
√
x
√
2· x + k
ex
ex + k
ex
ex + k
ex
ex + k
sin x
− cos x + k
sin x
− cos x + k
sin x
− cos x + k
cos x
sin x + k
cos x
sin x + k
cos x
sin x + k
http://chingatome.net
f (x)
F (x)
f (x)
F (x)
a
a·x + k
a
a·x + k
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
ln x + k
1
x2
1
− +k
x
1
x2
1
− +k
x
1
√
x
√
2· x + k
1
√
x
√
2· x + k
ex
ex + k
ex
ex + k
sin x
− cos x + k
sin x
− cos x + k
cos x
sin x + k
cos x
sin x + k
f (x)
F (x)
f (x)
F (x)
a
a·x + k
a
a·x + k
xn
1
·xn+1 + k
n+1
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
Pour x>0,
1
x
ln x + k
1
x2
1
− +k
x
1
x2
1
− +k
x
1
√
x
√
2· x + k
1
√
x
√
2· x + k
ex
ex + k
ex
ex + k
sin x
− cos x + k
sin x
− cos x + k
cos x
sin x + k
cos x
sin x + k
http://chingatome.net
f (x)
F (x)
f (x)
a
a·x + k
[
]n
n·u′ (x)· u(x)
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
1
x2
1
− +k
x
1
√
x
√
2· x + k
ex
ex + k
sin x
− cos x + k
cos x
u′ (x)
[
]2
u(x)
F (x)
[
−
où u(x) ̸= 0
u′ (x)·eu(x)
u′ (x)
u(x)
{
où
u′ (x)>0
u(x)>0
]n+1
u(x)
+k
1
+k
u(x)
eu(x) + k
[
]
ln u(x) + k
[
]
u′ (x)· sin u(x)
[
]
− cos u(x) + k
sin x + k
[
]
u′ (x)· cos u(x)
[
]
sin u(x) + k
f (x)
F (x)
f (x)
F (x)
a
a·x + k
[
]n
n·u′ (x)· u(x)
xn
1
·xn+1 + k
n+1
Pour x>0,
1
x
ln x + k
1
x2
1
− +k
x
1
√
x
√
2· x + k
ex
ex + k
sin x
− cos x + k
cos x
sin x + k
u′ (x)
[
]2
u(x)
où u(x) ̸= 0
u′ (x)·eu(x)
u′ (x)
u(x)
{
où
u′ (x)>0
u(x)>0
[
]n+1
u(x)
+k
−
1
+k
u(x)
eu(x) + k
[
]
ln u(x) + k
[
]
u′ (x)· sin u(x)
[
]
− cos u(x) + k
[
]
u′ (x)· cos u(x)
[
]
sin u(x) + k
http://chingatome.net