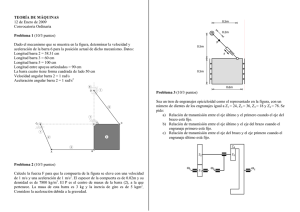
Análisis de velocidades y aceleraciones
Anuncio

Análisis de velocidades y aceleraciones Método del polígono Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Contando como dato con la 2, y sabiendo que el movimiento de la barra 2 es rotacional, se calcula la velocidad del punto A: VA=2 xr02-A VA = Velocidad tangencial de A. 2 = Velocidad angular de la barra 2. r02-A = Distancia deO2 a A. Se sabe también que el punto B tiene movimiento de traslación horizontal y al ser A y B puntos de la misma barra con movimiento combinado (biela) se puede plantear la ecuación de movimiento relativo.: VB=VA+VBA VB = Velocidad absoluta de B. VBA = Velocidad relativa de B con respecto de A. Habiendo resuelto las velocidades VB y VBA, se puede utilizar la VBA para calcular 3: 3=VBA/rA-B 3 = Velocidad angular de la barra 3. rA-B = Distancia de A a B. Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. VA Perpendicular a O2A Perpendicular a BA VBA VB Paralelo al movimiento de B OV Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Habiendo resuelto las velocidades VB y VBA, se puede utilizar la VBA para calcular 3: 3=VBA/rA-B 3 = Velocidad angular de la barra 3. rA-B = Distancia de A a B. Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Teniendo ya resuelta 3 se pueden seguir cualquiera de las siguientes dos ecuaciones de movimiento relativo, para calcular la velocidad de G: VG=VA+VGA VG = Velocidad absoluta de G. VGA = Velocidad relativa de G con respecto de A. VGA=3 xrA-G rA-G = Distancia de A a G. (Otra opción) VG=VB+VGB VGB = Velocidad relativa de G con respecto de B. VGB=3 xrB-G rB-G = Distancia de B a G. Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Perpendicular a GA VA Perpendicular a O2A VGB VG Sin dirección específica OV Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Si 2 es constante entonces α2=0 y la aceleración absoluta de A sería: aA=aNA +aTA aA= aceleración absoluta de A. aNA = aceleración normal de A. aTA = aceleración tangencial de A. aNA=(2 )2 r02-A aTA= α2xr02-A Se sabe también que el punto B tiene movimiento de traslación horizontal y al ser A y B puntos de la misma barra con movimiento combinado (biela) se puede plantear la ecuación de movimiento relativo.: aB=aA+aBA aB = aceleración absoluta de B. aBA = aceleración relativa de B con respecto de A. aBA=aNBA +aTBA aNBA = aceleración normal de B con respecto de A. aTBA = aceleración tangencial de B con respecto de A. aNBA=(3 )2 rA-B Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Paralelo al movimiento de B Oa aB Perpendicular a 3 aTBA Paralela a 2 y de A hacia O2A aNA aNBA Paralela a 3 y de B hacia A Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Habiendo resuelto las aceleraciones aB y aTBA, se puede utilizar la aTBA para calcular α3: α3=aTBA/rA-B α3 = aceleración angular de la barra 3. Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Teniendo ya resuelta α3 se pueden seguir cualquiera de las siguientes dos ecuaciones de movimiento relativo, para calcular la aceleración de G: aNGA=(3)2rA-G aTGA=α3xrA-G (otra opción) aG=aA+aGA aGB = aceleración relativa de G con respecto de B. aG = aceleración absoluta de G. aGA = aceleración relativa de G con respecto de A. aGA= aNGA+ aTGA aNGA = aceleración normal de G con respecto de A. aTGA = aceleración tangencial de G con respecto de A. aG=aB+aGB aGB= aNGB+ aTGB aNGB = aceleración normal de G con respecto de B. aTGB = aceleración tangencial de G con respecto de B. aNGB=(3)2rB-G aTGB=α3xrB-G Determine la velocidad y aceleración del punto G de la barra 3, en el instante mostrado, sabiendo que la barra 2 tiene una velocidad angular constante. Oa Sin dirección específica aG aTBA Perpendicular a 3 Paralela a 2 y de A hacia O2A aNA aNBA Paralela a 3 y de B hacia A