Tabla resumen de la distribución gamma
Anuncio
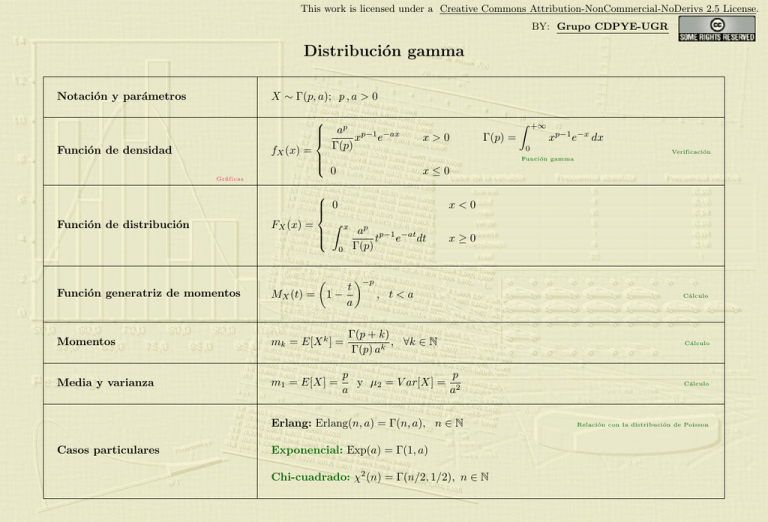
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 2.5 License. BY: Grupo CDPYE-UGR Distribución gamma X ∼ Γ(p, a); p , a > 0 Notación y parámetros Función de densidad fX (x) = ap p−1 −ax x e Γ(p) Z x>0 Γ(p) = +∞ xp−1 e−x dx 0 Verificación Función gamma x≤0 0 Gráficas Función de distribución 0 Z FX (x) = x<0 x 0 ap p−1 −at t e dt Γ(p) Función generatriz de momentos −p t MX (t) = 1 − , t<a a Momentos mk = E[X k ] = Media y varianza m1 = E[X] = x≥0 Γ(p + k) , ∀k ∈ N Γ(p) ak p p y µ2 = V ar[X] = 2 a a Erlang: Erlang(n, a) = Γ(n, a), n ∈ N Casos particulares Exponencial: Exp(a) = Γ(1, a) Chi-cuadrado: χ2 (n) = Γ(n/2, 1/2), n ∈ N Cálculo Cálculo Cálculo Relación con la distribución de Poisson











