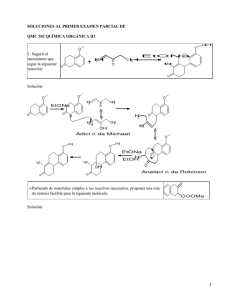
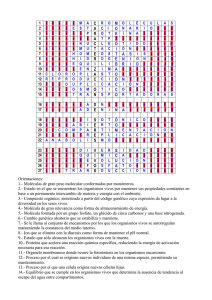
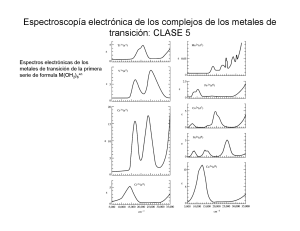
σ σ σ σ π π ω = θ ω θ θ =
Anuncio

ESPECTROSCOPIA 2 TRANSICIONES ELECTRÓNICAS EJERCICIOS 1) El símbolo del término del estado fundamental de N2+ es 2 Σ +g . Diga cual es el espín total y el momento angular orbital total de la molécula. Verifique que el símbolo del término coincide con lo que predice el principio de construcción. 2) Uno de los estados excitados de la molécula C2 tiene la configuración electrónica de valencia 1σ g21σ u2 2σ g2 2σ u21π u3 2π 1g . Obtenga la multiplicidad y la paridad del término. 3) Los aniones de las moléculas diatómicas homonucleares de halógenos presentan un estado fundamental 2 Σu+ y estados excitados 2 Π g , 2 Π u y 2 Σ +g . Indique las transiciones permitidas desde el estado fundamental. 4) El número de onda vibracional de la molécula de O2 en el estado fundamental es 1580 cm-1, mientras que el del primer estado excitado ( B 3Σu− ) vale 700 cm-1. La separación entre los mínimos de las curvas de energía electrónica es 6,175 eV. Calcule el número de onda de la transición entre los estados vibracionales más bajos de ambos estados electrónicos. Ignore la estructura rotacional y los efectos debidos a la anarmonicidad. 5) a) Identifique el grupo de simetría de la molécula de butadieno. b) Asigne la simetría a los orbitales moleculares Hückel obtenidos previamente. 6) Repita lo mismo con el benceno 7) Los factores de Franck-Condon se pueden calcular exactamente cuando se usa el modelo del oscilador armónico para los estados electrónicos fundamental y excitados que participan en la transición. Las constantes espectroscópicas relevantes son ω = k m y Re para el estado fundamental y ω ′ = k ′ m y Re′ = Re + d para el excitado. Si reemplazamos ω y ω ′ por su media armónica, aritmética o geométrica ω la expresión para los factores de Franck-Condon son aún más sencillos. En particular para las transiciones v′ = n ← v = 0 estos factores siguen la distribución de Poisson S0 n = θn eθ n ! , θ= mω d 2 , n = 0,1,… 2 a) Grafique S00 , S01 , S02 , y S03 en función de θ . b) Grafique S0n para la banda roja del CN ⎡⎣ A2 Π i (v′) ← X 2 Σ + (v) ⎤⎦ , (θ = 0, 7) c) Haga lo mismo con la transición ⎡⎣ A1Π (v′) ← X 1Σ + (v ) ⎤⎦ del CO (θ = 2,1)