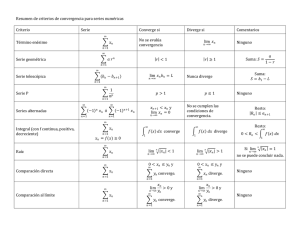
CRITERIOS DE COMPARACIÓN INTEGRALES IMPROPIAS

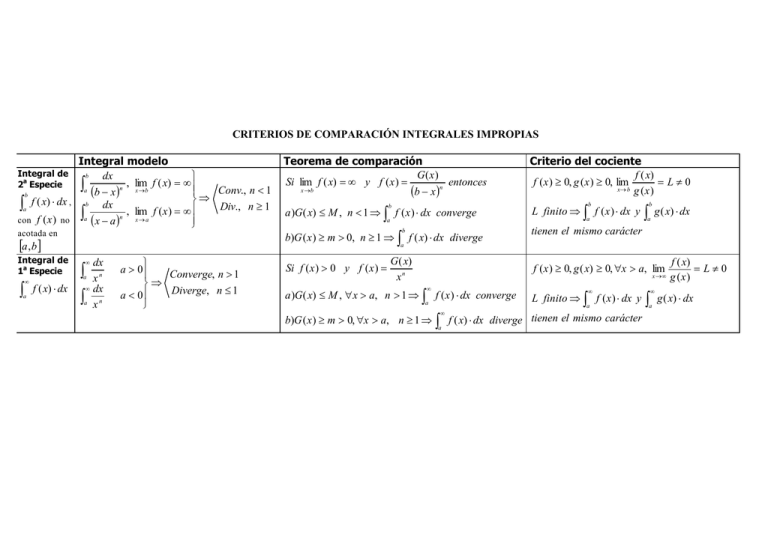
CRITERIOS DE COMPARACIÓN INTEGRALES IMPROPIAS
Integral modelo
b
dx

, lim f ( x) = ∞ 
∫
n
a
x →b
Conv., n < 1

(b − x )
b
⇒

f
(
x
)
⋅
dx
,
b
dx
∫a
Div., n ≥ 1
, lim f ( x ) = ∞ 
∫
n
a
x
→
a
con f (x ) no

(x − a)
Integral de
2a Especie
acotada en
[a, b ]
Integral de
1a Especie
∫
∞
a
f ( x) ⋅ dx
Teorema de comparación
G( x )
Si lim f ( x) = ∞ y f ( x ) =
entonces
x →b
(b − x )n
Criterio del cociente
f ( x)
f ( x ) ≥ 0, g ( x ) ≥ 0, lim
=L≠0
x→ b g ( x )
a )G( x) ≤ M , n < 1 ⇒ ∫ f ( x ) ⋅ dx converge
L finito ⇒ ∫ f ( x ) ⋅ dx y
b)G ( x ) ≥ m > 0, n ≥ 1 ⇒ ∫ f ( x) ⋅ dx diverge
tienen el mismo carácter
b
a
b
b
a
∫
b
a
g ( x) ⋅ dx
a
∞
dx
∫a x n
∞ dx
∫a x n

a > 0
Converge, n > 1
⇒
Diverge, n ≤ 1
a < 0

Si f ( x ) > 0 y f ( x ) =
G( x)
xn
f ( x ) ≥ 0, g ( x) ≥ 0, ∀x > a, lim
x →∞
∞
a )G( x) ≤ M , ∀ x > a, n > 1 ⇒ ∫ f ( x ) ⋅ dx converge
a
b)G ( x ) ≥ m > 0, ∀x > a, n ≥ 1 ⇒
∫
∞
a
∞
L finito ⇒ ∫ f ( x ) ⋅ dx y
a
f ( x) ⋅ dx diverge tienen el mismo carácter
∫
∞
a
f ( x)
=L≠0
g (x )
g ( x) ⋅ dx