Laboratorio 3 - Control inteligente
Anuncio

CONTROL INTELIGENTE
Laboratorio Nº3 CONTROL DE PLANTAS CON REDES NEURONALES
Profesor: Juan Pablo Rivera.
Objetivos
Definir la arquitectura de una Red Neuronal que permita realizar el control
de dos motores que definen el desplazamiento de un robot básico.
Entrenar una Red Neuronal para que resuelvan un problema con
parámetros linealmente separables.
Validar el modelo que se tiene con una Red Neuronal luego de entrenarla
con los datos provenientes de la planta.
DETECCIÓN DE OBSTÁCULOS PARA UN ROBOT
DESCRIPCIÓN DEL PROBLEMA
Un robot cuenta con cuatro sensores de proximidad en distintas ubicaciones
que permanentemente detectan si hay objetos en una distancia superior o
inferior a la preestablecida. Con base en esto, se decide si se da marcha
adelante o atrás con cada uno de los dos motores que posee. Para las
entradas, tenga en cuenta que un objeto cercano es presentado por un sensor
como un 1, y un objeto lejano como un ‐1. En la salida, la marcha hacia
adelante se presenta como un 1 y la marcha hacia atrás como un ‐1. La tabla
presenta el comportamiento deseado del robot para siete posibles entradas.
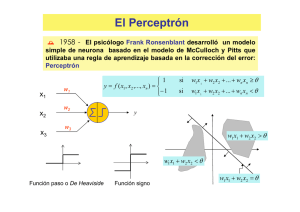
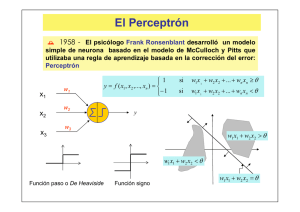
1. Arquitectura de la Red a implementar. Dada la simplicidad del problema
(salidas binarias y número de posibles combinaciones de entrada
conocido), su puede pensar en resolver el sistema con una Red tipo
perceptrón.
Para este perceptrón utilizaremos una función ‘Hardlims’ ya que este tipo de
función de activación nos entrega dos posibles salidas que son uno(1) o menos
uno (-1) según sea la entrada a esta; además este tipo de salidas son las
requeridas en el proceso para enviar la señal a los motores para permitir el
avance o retroceso del robot dependiendo de la cercanía o no de un objeto.
El software implementado para entrenar este perceptrón es el siguiente:
clear all
clc
X=[1 1 1 1;-1 1 1 1;1 1 -1 -1;-1 -1 -1 -1;1 -1 1 1;1 1 -1 1;1 1 1 -1]'
%defino el vector de entradas.
D=[-1 -1;-1 1;1 -1;1 1;1 -1;-1 1;1 -1]'; %defino el vector de salidas.
red=newp([-1 1;-1 1;-1 1;-1 1],2,'hardlims')%defino los valores max y
min en las entradas y el numero de capas de salida=2, además de la
función de activación hardlims.
tic %Comienzo a cronometrar el entrenamiento del perceptrón.
red.iw{1,1}=rand(2,4);%selecciono aleatoriamente los pesos de las 2
neuronas con las 4 entradas
red.b{1}=[0.5;0.5];
);%selecciono
los
pesos
de
las
2
bias
red.adaptParam.passes=20 );%Delimito un limite de repeticiones para el
entrenamiento del perceptrón.
red=adapt(red,X,D) %Adapto la red de acuerdo a los patrones de
entrenamiento.
Toc %Finalizo el conteo de tiempo para ver cuánto se demoro en
entrenar el perceptrón.
in_prueba=[1;1;-1;1]%Patrón de prueba para determinar la efectividad
del perceptrón.
b=sim(red,in_prueba) %Simulo con los valores de prueba y compruebo los
valores si son los deseados.
Explicación de comandos utilizados para el software
a)
b)
c)
d)
e)
f)
newp, para definir la arquitectura de la red
net.IW{1,1}, para definir o llamar un vector de pesos
net.b{1}, para definir o llamar un vector de umbrales
net.adaptParam.passes, para definir el número de iteraciones máximo.
adapt, para entrenar
sim, para simular la red con el vector de pesos final (después de haber
entrenado).
g) rand, selección aleatoria de valores de los vectores de pesos.
2. ANALISIS DE LA RED ANTE PATRONES DE ENTRADA PARA LOS QUE
NO FUE ENTRENADA.
La red solo fue entrenada con 7 de las 16 posibles combinaciones de entradas,
por lo que se prueba la red para los valores de entrada que no fue entrenada;
estos valores son presentados a continuación:
S1
-1
-1
-1
-1
-1
-1
1
1
1
S2
-1
-1
-1
1
1
1
-1
-1
-1
S3
-1
1
1
-1
-1
1
-1
-1
1
S4
1
-1
1
-1
1
-1
-1
1
-1
M1
-1
1
-1
1
-1
1
1
1
1
M2
1
-1
1
1
1
-1
-1
1
-1
Con base a la tabla anterior se puede afirmar que la red no memoriza sino que
generaliza, ya que estos valores no se tuvieron en cuenta para entrenar la red,
y sin embargo la red ante esta combinación de entradas no presenta un estado
de error y por el contrario entrega una salida para cada uno de los motores.
Es de notar que la red ante un vector de pesos de diferente no varía en su
comportamiento final, ya que este siempre se está modificando hasta obtener
un vector de pesos ideal para el comportamiento de la red, es decir, hasta que
se acomode de manera casi ideal al comportamiento del robot.
El tiempo de ejecución de este perceptrón fue en promedio 0.8 segundos sin
importar el vector de pesos de entrada.
CONCLUSIONES
Como las salidas esperadas son iguales a las obtenidas, entonces
podemos afirmar que el vector de pesos obtenido es el ideal para el
funcionamiento del robot y por tanto la red ha quedado bien entrenada.
Debido a que el problema es linealmente separable se pudo utilizar un
perceptrón, el cual con una función de activación diferente a la función
“Hardlims” no entregaba los valores esperados en la salida.
Una red neuronal es un sistema que no es memorístico sino que este
generaliza de acuerdo a las entradas de la neurona, ya que ante nuevos
patrones de entrada para los cuales no fue entrenada, la red entrega una
respuesta lógica al sistema a controlar.
El seleccionar o no un vector de pesos inicial para la neurona parece no
tener gran relevancia, ya que si este no es el vector de pesos adecuado la
red automáticamente ira modificando este hasta conseguir el vector de
pesos ideal para el proceso.