Document
Anuncio
El Perceptrón
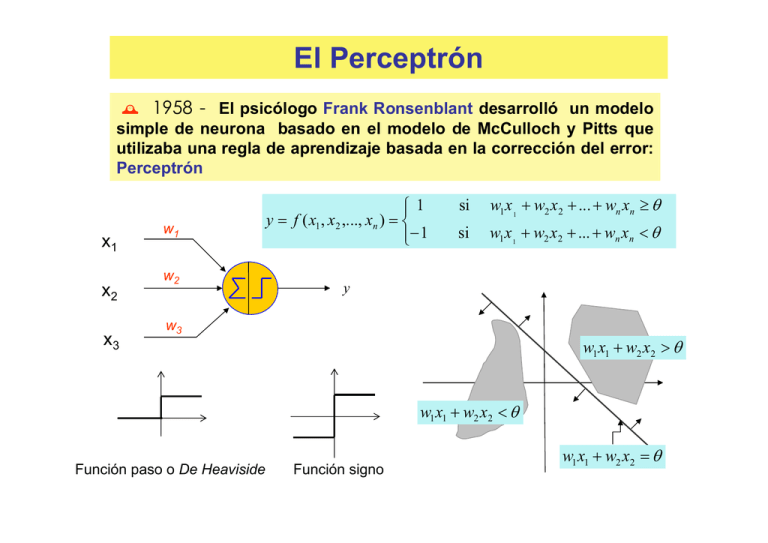
´ 1958 - El psicólogo Frank Ronsenblant desarrolló un modelo
simple de neurona basado en el modelo de McCulloch y Pitts que
utilizaba una regla de aprendizaje basada en la corrección del error:
Perceptrón
x1
x2
x3
w1
w2
1
y = f ( x1 , x2 ,..., xn ) =
− 1
si
w1 x1 + w2 x2 + ... + wn xn ≥ θ
si
w1 x 1 + w2 x2 + ... + wn xn < θ
y
w3
w1 x1 + w2 x2 > θ
w1 x1 + w2 x2 < θ
Función paso o De Heaviside
Función signo
w1 x1 + w2 x2 = θ
¿Qué se pretende con el Perceptrón?
Se dispone de la siguiente información:
L Conjunto de patrones {xk}, k = 1,2,…,p1 , de la clase C1
(zk = 1)
L Conjunto de patrones {xr}, k = p1+1,...,p , de la clase C2
(zr = -1)
Se pretende que el perceptrón asigne a cada entrada (patrón xk) la
siguiendo un proceso de corrección de error
salida deseada zk
(aprendizaje) para determinar los pesos sinápticos apropiados
Regla de aprendizaje del Perceptrón:
w j (k ) + 2ηx j (k )
w j (k + 1) = w j (k )
w j (k ) − 2ηx j (k )
∆w j (k ) = η (k )[z (k ) − y (k )]x j (k )
si y (k ) = −1 y z (k ) = 1,
si y (k ) = z (k )
si y (k ) = 1 y z (k ) = −1
error
tasa de
aprendizaje
¿Cómo se modifica el sesgo θ ?
w1 x1 + w2 x2 + ... + wn xn ≥ θ
x1
x2
x3
−1
⇔ w1 x1 + w2 x2 + ... + wn xn + wn+1 xn+1 ≥ 0
w1
w2
θ
y
w1 x1 + w2 x2 + ... + wn xn + θ (−1) ≥ 0
w3
θ
−1
∆θ (k ) = −η (k )[z (k ) − y (k )]
Algoritmo del Perceptrón
Paso 0: Inicialización
Inicializar los pesos sinápticos con números aleatorios del intervalo [-1,1].
Ir al paso 1 con k=1
Paso 1: (k-ésima iteración)
n+1
Calcular
y(k ) = sgn ∑ w j x j (k )
j =1
Paso 2: Corrección de los pesos sinápticos
Si z(k) ≠ y(k) modificar los pesos sinápticos según la expresión:
w j (k + 1) = w j (k ) + η [z i (k ) − y i (k )]x j (k ) ,
j = 1,2,..., n + 1
Paso 3: Parada
Si no se han modificado los pesos en las últimas p iteraciones, es decir,
w j (r ) = w j (k ), j = 1,2,..., n + 1, r = k + 1,..., k + p
parar. La red se ha estabilizado.
En otro caso, ir al Paso 1 con k=k+1.
El perceptron con Bolsillo
Consiste en tener en cuenta el número de iteraciones consecutivas del
algoritmo de perceptrón en las cuales no se ha modificado el vector de
pesos sinápticos (para cada uno de los vectores que va generando), es
decir, tener en cuenta el número de patrones que se han clasificado
correctamente con dicho vector hasta que se ha encontrado el primer
patrón que clasifica incorrectamente. Se tiene “guardado en el bolsillo” la
mejor solución explorada, es decir, el vector de pesos sinápticos
generado que ha conseguido, hasta el momento, el mayor número de
iteraciones sin ser modificado. Cuando se encuentra un nuevo vector de
pesos sinápticos que consigue un mayor número de clasificaciones
correctas consecutivas que el que hay en el bolsillo entonces el vector
del bolsillo se reemplaza por este. La solución final viene dada por el
vector de pesos sinápticos guardado en el bolsillo.
Algoritmo
del
Perceptrón
con
bolsillo
La ADALINA
La ADALINA (también llamada ADALINE), pues corresponde al acrónimo
de ADAptive Linear NEuron) o neurona con adaptación lineal que fue
introducida por Widrow en 1959. Esta neurona es similar al Perceptrón
simple pero utiliza como función de transferencia la función identidad en
lugar de la función signo. La salida de la ADALINA es simplemente una
función lineal de las entradas (ponderadas con los pesos sinápticos):
N
y = ∑ wj x j −θ
j =1
N +1
y = ∑ wj x j
j =1
{x , x
1
2
,..., x
p
} {z
1
2
, z ,..., z
p
}
E=
p
(
)
1
z k − y (k )
∑
2 k =1
2
1 k N +1
= ∑ z − ∑ w j (k ) x kj
2 k =1
j =1
p
2
La ADALINA
Aprendizaje individualizado:
E=
p
(
)
2
1
k
(
)
z
y
k
−
∑
2 k =1
wr (k + 1) = wr (k ) + ∆wr (k )
[
]
= η z k − y (k ) x rk
1 k N +1
k
= ∑ z − ∑ w j (k ) x j
2 k =1
j =1
p
∂E
∆wr (k ) = −η
∂wr (k )
2
La ADALINA
Aprendizaje por lotes:
E=
p
(
)
2
1
k
(
)
z
y
k
−
∑
2 p k =1
k N +1
1
k
z − ∑ w j x j
=
∑
2 p k =1
j =1
p
2
wr (k + 1) = wr (k ) + ∆wr (k )
[
]
1 p k
= η ∑ z − y (k ) x kj
p k =1
∂E
∆wr (k ) = −η
∂wr (k )
Adalina
Para tratar problemas de clasificación suele ponerse una función signo al
final de la salida continua. Sin embargo todos los cálculos del proceso
de entrenamiento se realizan con la salida continua.
Neuronas con salida continua:
Regla de aprendizaje de Widrow-Hoff ó
Regla delta ó regla LMS (least mean square)
x1
x2
x3
w1
w2
w3
y
N
y = g ∑ w j x j
j =1
g (x ) ≡
1
1 + exp(− 2 βx )
e β x − e−β x
g ( x ) = tanh (βx ) = β x
e + e −β x
Neuronas con salida continua:
Regla de aprendizaje de Widrow-Hoff
en linea
E=
p
(
)
2
1
k
(
)
z
y
k
−
∑
2 k =1
∆w j (k ) = −η
∂E
∂w j (k )
Descenso por el gradiente
N +1
1 k
k
= ∑ z − g (∑ w j (k ) x j )
2 k =1
j =1
p
[
]
= η z k − y (k ) g ' (h )x kj
2
1
g (x ) ≡
1 + exp(− 2 βx )
Calcular g’(x) para estos dos casos
e β x − e−β x
g ( x ) = tanh (βx ) = β x
e + e −β x
1
g (x ) ≡
1 + exp(− 2 βx )
g’(x)= 2 B g(x) (1-g(x))
e β x − e−β x
g ( x ) = tanh (βx ) = β x
e + e −β x
g’(x)= B [1 –g2(x)]
Neuronas con salida continua:
Regla de aprendizaje de Widrow-Hoff
por lotes (batch)
E=
p
(
)
2
1
k
(
)
z
y
k
−
∑
2 p k =1
∂E
∆w j = −η
∂w j
N +1
k
1
k
z − g (∑ w j x j )
=
∑
2 p k =1
j =1
p
[
2
]
1 p k
= η ∑ z − y (k ) g ' (h) x kj
p k =1
Ventajas de aprendizaje en línea o por lotes:
En-linea: Menor computación, cierta aleatoriedad ayuda a escapar de mínimos,
No requiere datos estáticos
Por lotes(Batch): es simple y determinista (repetible).
Convergencia: similar pero puede depender del algoritmo en cuestión.
Regla
Salida
Perceptrón bipolar
(+1;-1)
Perceptrón bipolar
+
(+1;-1)
Bolsillo
Continua
Adaline
Aprendizaje Convergencia
Corrección
errores
Corrección
errores +
memoria
Descenso
y/o( +1;-1)
gradiente
WidrowContinua Descenso
Hoff (LMS)
gradiente
LS: OK
NLS: oscila
LS:OK
NLS: OK
converge
cte. pequeña
converge
cte. pequeña