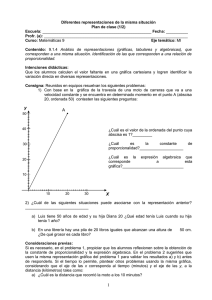
G9B5C5 - Siplandi
Anuncio

Plan de clase (1/3) Escuela: ______________________________________ Fecha: ________________ Profesor (a): _________________________________________________________ Curso: Matemáticas 9 Eje temático: MI Contenido: 9.5.5 Análisis de situaciones problemáticas asociadas a fenómenos de la física, la biología, la economía y otras disciplinas, en las que existe variación lineal o cuadrática entre dos conjuntos de cantidades. Intenciones didácticas: Que los alumnos relacionen dos conjuntos de datos que guardan una relación lineal o cuadrática y determinen la expresión algebraica que modela dicha relación. Consigna: Individualmente resuelvan los siguientes problemas. 1. Una persona tiene la presión arterial alta y el médico se la quiere nivelar. El médico sabe que 1 mg de cierta medicina disminuye 1.5 unidades de presión. Si y representa la disminución en la presión y x el número de miligramos que se receta, escribe algebraicamente la relación entre x y y. 2. Cristina tiene 3 años menos que Andrés. Si representamos por y la edad de Cristina y por x la edad de Andrés, escribe algebraicamente la relación entre x y y. 3. Se deja caer una pelota desde la parte alta de un edificio, si en el primer segundo recorre 4.9 m, en el segundo 19.6 y en tercero 44.1, ¿qué expresión algebraica permite calcular la distancia (d), en función del tiempo (t)? 4. Tres empresas rentan fotocopiadoras. Por el alquiler de un equipo, la empresa 1 cobra $ 3 000.00 al mes y $ 50.00 por hora de uso; la empresa 2 cobra $ 75.00 por cada hora de uso y la empresa 3 cobra $ 2 500.00 al mes y $ 65.00 por hora de uso. Escribe una expresión algebraica para cada caso, en la que se relacione el cobro mensual (C) de cada empresa en función del número de horas (h) de uso. Consideraciones previas: Las situaciones de este plan están escritas en lenguaje común. Se trata de analizarlas para identificar las magnitudes involucradas y el tipo de variación entre ellas (lineal o cuadrática), con la finalidad de escribirlas algebraicamente. Una vez que se han identificado las variables de una situación, si los alumnos tienen problemas para buscar la relación entre ellas, se les puede sugerir que construyan con ellas una tabla, ésta facilita la búsqueda de su relación. Por ejemplo, para el problema 3 se puede elaborar la siguiente tabla: Tiempo en segundos. (t) 1 2 3 Distancia recorrida en metros. (d) 4.9 19.6 44.1 Con la finalidad de focalizar aún más la atención puede plantearse la siguiente pregunta: ¿qué operaciones tiene que hacerse a la magnitud tiempo para obtener la correspondiente distancia recorrida? El propósito es que llegan a identificar que la distancia es igual al cuadrado del tiempo por la constante 4.9. La expresión algebraica de esta variación cuadrática es d = 4.9 t2. Una de las finalidades de obtener la fórmula es que a partir de ella se pueden calcular otros valores, por lo tanto, se sugiere plantear otras preguntas, como por ejemplo, ¿cuál es la distancia recorrida después de 7 segundos? ¿en qué tiempo tardaría en caer al suelo la pelota si la altura del edificio fuera 122.5 m? A excepción de la situación 3, las demás se tratan de variaciones lineales, vale la pena distinguir entre ellas las que representan una relación de proporcionalidad, la que hace referencia a la presión arterial y la que se refiere al cobro de la empresa 2, e identificar las diferencias en la escritura de sus expresiones algebraicas. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Plan de clase (2/3) Escuela: ______________________________________ Fecha: _______________ Profesor (a): _________________________________________________________ Curso: Matemáticas 9 Eje temático: MI Contenido: 9.5.5 Análisis de situaciones problemáticas asociadas a fenómenos de la física, la biología, la economía y otras disciplinas, en las que existe variación lineal o cuadrática entre dos conjuntos de cantidades. Intenciones didácticas: Que los alumnos analicen variaciones lineales y cuadráticas representadas mediante una expresión algebraica, una tabla o en lenguaje común y representen dichas relaciones gráficamente. Consigna: Individualmente resuelve los siguientes problemas. Utiliza tu cuaderno para hacer las gráficas. 1. Una piscina se está vaciando a fin de limpiarla. Por el desagüe se desalojan 60 litros cada minuto. Tiene 1800 litros de contenido en el momento en que comienza el vaciado. Haz una gráfica que represente la relación tiempo (minutos) y la cantidad de agua (litros) contenida en la piscina. 2. Dada la expresión y = 2x2 + 3, dibuja la gráfica que represente la relación entre x y y. 3. Un autobús se desplaza a una velocidad constante. En la siguiente tabla se registran algunas distancias recorridas y sus correspondientes tiempos. Tiempo (h) Distancia (km) 0.5 160 3.5 280 6 10 560 Calcula los valores faltantes de la tabla y elabora una gráfica que represente la relación entre el tiempo (x) y la distancia (y) de esta situación. Consideraciones previas: Es recomendable vincular las diferentes representaciones de una variación lineal o cuadrática, de ahí que las situaciones de este plan se presentan de diversas maneras; mediante una expresión algebraica, mediante una tabla o bien en lenguaje común. Se sugiere aprovechar las gráficas que elaboren los alumnos para plantear algunas preguntas; por ejemplo, en la primera situación se puede preguntar, ¿cuántos litros de agua se desalojaron en un cuarto de hora? ¿en cuánto tiempo se termina de vaciar la piscina? Para contestar pueden utilizar la gráfica o bien manipular la expresión y = 1800 – 60x, en donde y representa la cantidad de agua en la piscina y x el número de minutos transcurridos. También se les puede solicitar a los alumnos que elaboren otras preguntas que puedan contestarse con la información de la gráfica. Es recomendable que desde el análisis del texto, la expresión algebraica o la tabla de valores, y antes de realizar las gráficas, los alumnos anticipen algunas características de las mismas, por ejemplo, ¿se trata de una recta o de una parábola? ¿pasa por el origen del plano cartesiano? Si se tiene una calculadora graficadora vale la pena utilizarla. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Plan de clase (3/3) Escuela: ______________________________________ Fecha: _______________ Profesor (a): _________________________________________________________ Curso: Matemáticas 9 Eje temático: MI Contenido: 9.5.5 Análisis de situaciones problemáticas asociadas a fenómenos de la física, la biología, la economía y otras disciplinas, en las que existe variación lineal o cuadrática entre dos conjuntos de cantidades. Intenciones didácticas: Que los alumnos relacionen gráficas de variaciones lineales y cuadráticas con sus respectivas representaciones algebraicas. Consigna: De manera individual identifica la gráfica que corresponda a cada una de las funciones señaladas en la tabla, escribe el número de gráfica en la segunda columna. Función Gráfica 1 y x 2 y 2x 3 y 3x 2 Consideraciones previas: La expectativa es que los alumnos identifiquen los dos tipos de representaciones, la gráfica y la algebraica, que corresponden a la misma relación; para ello, es deseable que los alumnos recurran al análisis de las características de dichas representaciones. Algunas características que posiblemente los alumnos pueden analizar son: a) para el caso de una relación de proporcionalidad, su gráfica es una recta que necesariamente pasa por el origen del plano cartesiano y su expresión algebraica es de la forma y = kx; b) para las funciones lineales que no representan una relación de proporcionalidad, son de la forma y=kx + b donde b es la ordenada al origen y c) para las variaciones cuadráticas, sus gráficas son parábolas. Para los tres casos, la pendiente es otro aspecto que se puede analizar pues entre mayor sea, se aleja más del eje de las abscisas. No se descartan otras posibles estrategias: Averiguar las coordenadas de un punto de la gráfica y sustituirlas en la expresión algebraica, si la satisface, entonces representan la misma relación y se corresponden. A partir de la expresión algebraica, determinar algunas parejas de valores (x, y) y ubicarlas en el plano cartesiano, si coinciden con el punto de una gráfica, entonces ésta y la expresión algebraica se corresponden. Será importante que si los alumnos no recurren al análisis de las características de las representaciones algebraicas y gráficas, sea el profesor quien proponga dicho análisis. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre