β γ γ β β β β γ β β β γ

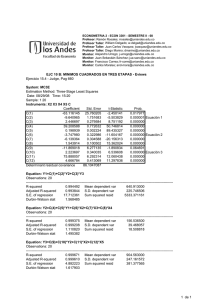
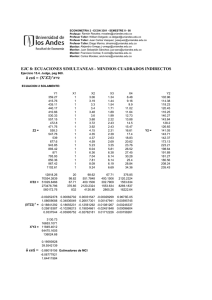
ECONOMETRIA 2 - ECON 3301 - SEMESTRE II - 08
Profesor: Ramón Rosales; rrosales@uniandes.edu.co
Profesor Taller: William Delgado; w-delgad@uniandes.edu.co
Profesor Taller: Juan Carlos Vasquez; jvasquez@uniandes.edu.co
Profesor Taller: Diego Marino; dmarino@uniandes.edu.co
Monitor: Alejandro Urrego; j-urrego@uniandes.edu.co
Monitor: Juan Sebastián Sánchez; jua-sanc@uniandes.edu.co
Monitor: Francisco Correa; fr-corre@uniandes.edu.co
Monitor: Carlos Morales; and-mora@uniandes.edu.co
EJC 5: ECUACIONES SIMULTÁNEAS: MINIMOS CUADRADOS ORDINARIOS,
MÍNIMOS CUADRADOS EN DOS ETAPAS Y MINIMOS CUADRADOS EN TRES
ETAPAS.
Considere el ejemplo 15.4 del libro de Judge et. al. (pag. 656) en el cual se tiene el
siguiente sistema de tres ecuaciones simultáneas (15.4.1.a.):
y1 = y 2 γ 21 + y 3γ 31 + x1 β11 + e1
y 2 = y1γ 12 + x1 β12 + x 2 β 22 + x3 β 32 + x 4 β 42 + e2
y 3 = y 2 γ 23 + x1 β 13 + x 2 β 23 + x5 β 53 + e3
Se tiene los siguientes datos de cada una de las variables con las cuales se desea efectuar la
estimación de las ecuaciones mediante mínimos cuadrados ordinarios, mínimos cuadrados
en dos etapas y mínimos cuadrados en tres etapas.
Base de datos. (Tabla 15.1 Pag. 657. Judge)
Y1
Y2
Y3
X1
X2
X3
X4
X5
359.27
102.96
578.49
1
3.06
1.34
8.48
28
415.76
114.38
650.86
1
3.19
1.44
9.16
35
435.11
118.23
684.87
1
3.3
1.54
9.9
37
440.17
120.45
680.47
1
3.4
1.71
11.02
36
410.66
116.25
642.19
1
3.48
1.89
11.64
29
530.33
140.27
787.41
1
3.6
1.99
12.73
47
557.15
143.84
818.06
1
3.68
2.22
13.88
50
472.8
128.2
712.16
1
3.72
2.43
14.5
35
471.76
126.65
722.23
1
3.92
2.43
15.47
33
538.3
141.05
811.44
1
4.15
2.31
16.61
40
547.76
143.71
816.36
1
4.35
2.39
17.4
38
539
142.37
807.78
1
4.37
2.63
18.83
37
677.6
173.13
983.53
1
4.59
2.69
20.62
56
943.85
223.21
1292.99
1
5.23
3.35
23.76
88
893.42
198.64
1179.64
1
6.04
5.81
26.52
62
871
191.89
1134.78
1
6.36
6.38
27.45
51
793.93
181.27
1053.16
1
7.04
6.14
30.28
29
850.36
180.56
1085.91
1
7.81
6.14
25.4
22
967.42
208.24
1246.99
1
8.09
6.19
28.84
38
1102.61
235.43
1401.94
1
9.24
6.69
34.36
41
1
Procedimiento en Stata
. * Estimación por el método de mínimos cuadrados ordinarios (ecuación
por ecuación). Note que X1 hace las veces del intercepto en cada ecuación.
. * Primera ecuación:
. reg y1 y2 y3
Source |
SS
df
MS
-------------+-----------------------------Model |
964394.6
2
482197.3
Residual |
3873.5508
17 227.855929
-------------+-----------------------------Total |
968268.15
19 50961.4816
Number of obs
F( 2,
17)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
= 2116.24
= 0.0000
= 0.9960
= 0.9955
= 15.095
-----------------------------------------------------------------------------y1 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y2 | -6.036774
1.424078
-4.24
0.001
-9.041316
-3.032231
y3 |
1.871742
.2274043
8.23
0.000
1.391961
2.351524
_cons | -107.2205
21.95716
-4.88
0.000
-153.546
-60.89489
------------------------------------------------------------------------------
. * Segunda ecuación:
. reg y2 y1 x2 x3 x4
Source |
SS
df
MS
-------------+-----------------------------Model | 29579.3426
4 7394.83564
Residual |
17.481556
15 1.16543706
-------------+-----------------------------Total | 29596.8241
19 1557.72759
Number of obs
F( 4,
15)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
= 6345.12
= 0.0000
= 0.9994
= 0.9993
= 1.0796
-----------------------------------------------------------------------------y2 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y1 |
.1961503
.0036274
54.07
0.000
.1884186
.203882
x2 | -3.867653
.517631
-7.47
0.000
-4.970958
-2.764349
x3 | -6.064856
.4781135
-12.68
0.000
-7.08393
-5.045781
x4 |
1.639327
.1377964
11.90
0.000
1.345621
1.933033
_cons |
39.53617
1.054067
37.51
0.000
37.28948
41.78286
------------------------------------------------------------------------------
. * Tercera ecuación:
. reg y3 y2 x2 x5
Source |
SS
df
MS
-------------+-----------------------------Model | 1160385.73
3 386795.245
Residual | 302.302875
16 18.8939297
-------------+-----------------------------Total | 1160688.04
19 61088.8441
Number of obs
F( 3,
16)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
=20471.93
= 0.0000
= 0.9997
= 0.9997
= 4.3467
-----------------------------------------------------------------------------y3 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y2 |
1.38193
.4278765
3.23
0.005
.4748724
2.288988
x2 |
90.96062
7.753938
11.73
0.000
74.52301
107.3982
x5 |
5.794933
.5601903
10.34
0.000
4.607383
6.982484
_cons | -1.355566
6.911302
-0.20
0.847
-16.00687
13.29574
------------------------------------------------------------------------------
2
. * Estimación por el método de mínimos cuadrados en dos etapas
(ecuación por ecuación). Note que todas las variables exógenas en el sistema se incluyen
como lista de variables instrumentales.
. * Primera ecuación:
. ivreg y1 (y2 y3 = x2 x3 x4 x5), first
First-stage regressions
-----------------------
Source |
SS
df
MS
-------------+-----------------------------Model | 29569.0989
4 7392.27472
Residual | 27.7252629
15 1.84835086
-------------+-----------------------------Total | 29596.8241
19 1557.72759
Number of obs
F( 4,
15)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
= 3999.39
= 0.0000
= 0.9991
= 0.9988
= 1.3595
-----------------------------------------------------------------------------y2 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------x2 |
17.40785
.7146592
24.36
0.000
15.88459
18.93111
x3 | -3.314505
.6122153
-5.41
0.000
-4.619411
-2.009599
x4 |
1.014514
.1827241
5.55
0.000
.625047
1.403981
x5 |
1.2081
.0281782
42.87
0.000
1.14804
1.268161
_cons |
12.5467
1.628307
7.71
0.000
9.07605
16.01736
------------------------------------------------------------------------------
Source |
SS
df
MS
-------------+-----------------------------Model | 1160510.91
4 290127.727
Residual | 177.130617
15 11.8087078
-------------+-----------------------------Total | 1160688.04
19 61088.8441
Number of obs
F( 4,
15)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
=24568.96
= 0.0000
= 0.9998
= 0.9998
= 3.4364
-----------------------------------------------------------------------------y3 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------x2 |
117.7659
1.806375
65.19
0.000
113.9157
121.6161
x3 | -7.908896
1.547438
-5.11
0.000
-11.20718
-4.610611
x4 |
1.556596
.461854
3.37
0.004
.5721772
2.541014
x5 |
7.46698
.0712234
104.84
0.000
7.315171
7.618789
_cons |
10.67843
4.115715
2.59
0.020
1.905989
19.45087
-----------------------------------------------------------------------------Instrumental variables (2SLS) regression
Source |
SS
df
MS
-------------+-----------------------------Model | 963117.025
2 481558.513
Residual | 5151.12518
17 303.007364
-------------+-----------------------------Total |
968268.15
19 50961.4816
Number of obs
F( 2,
17)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
= 1596.41
= 0.0000
= 0.9947
= 0.9941
= 17.407
-----------------------------------------------------------------------------y1 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y2 | -9.408592
1.959456
-4.80
0.000
-13.54268
-5.274501
y3 |
2.409556
.3127735
7.70
0.000
1.749661
3.06945
_cons | -65.89405
28.52199
-2.31
0.034
-126.0702
-5.717905
-----------------------------------------------------------------------------Instrumented: y2 y3
Instruments:
x2 x3 x4 x5
------------------------------------------------------------------------------
3
. * Segunda ecuación:
. ivreg y2 (y1 = x2 x3 x4 x5) x2 x3 x4, first
First-stage regressions
----------------------Source |
SS
df
MS
-------------+-----------------------------Model | 968192.206
4 242048.052
Residual | 75.9439522
15 5.06293015
-------------+-----------------------------Total |
968268.15
19 50961.4816
Number of obs
F( 4,
15)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
=47807.90
= 0.0000
= 0.9999
= 0.9999
= 2.2501
-----------------------------------------------------------------------------y1 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------x2 |
108.544
1.18279
91.77
0.000
106.023
111.0651
x3 |
14.05168
1.013241
13.87
0.000
11.89201
16.21135
x4 | -3.213271
.3024158
-10.63
0.000
-3.857855
-2.568687
x5 |
6.165687
.0466362
132.21
0.000
6.066285
6.26509
_cons | -137.8361
2.694915
-51.15
0.000
-143.5802
-132.092
------------------------------------------------------------------------------
Instrumental variables (2SLS) regression
Source |
SS
df
MS
-------------+-----------------------------Model | 29579.3386
4 7394.83466
Residual | 17.4854997
15 1.16569998
-------------+-----------------------------Total | 29596.8241
19 1557.72759
Number of obs
F( 4,
15)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
= 6341.49
= 0.0000
= 0.9994
= 0.9993
= 1.0797
-----------------------------------------------------------------------------y2 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y1 |
.1959393
.0036294
53.99
0.000
.1882034
.2036752
x2 | -3.860193
.517703
-7.46
0.000
-4.96365
-2.756735
x3 | -6.067781
.4781697
-12.69
0.000
-7.086976
-5.048587
x4 |
1.64412
.1378331
11.93
0.000
1.350336
1.937905
_cons |
39.55421
1.054225
37.52
0.000
37.30718
41.80124
-----------------------------------------------------------------------------Instrumented: y1
Instruments:
x2 x3 x4 x5
-----------------------------------------------------------------------------. * Tercera ecuación:
ivreg y3 (y2 = x2 x3 x4 x5) x2 x5, first
First-stage regressions
----------------------Source |
SS
df
MS
-------------+-----------------------------Model | 29569.0989
4 7392.27472
Residual | 27.7252629
15 1.84835086
-------------+-----------------------------Total | 29596.8241
19 1557.72759
Number of obs
F( 4,
15)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
= 3999.39
= 0.0000
= 0.9991
= 0.9988
= 1.3595
-----------------------------------------------------------------------------y2 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------x2 |
17.40785
.7146592
24.36
0.000
15.88459
18.93111
x5 |
1.2081
.0281782
42.87
0.000
1.14804
1.268161
x3 | -3.314505
.6122153
-5.41
0.000
-4.619411
-2.009599
x4 |
1.014514
.1827241
5.55
0.000
.625047
1.403981
_cons |
12.5467
1.628307
7.71
0.000
9.07605
16.01736
------------------------------------------------------------------------------
4
Instrumental variables (2SLS) regression
Source |
SS
df
MS
-------------+-----------------------------Model | 1160353.61
3 386784.536
Residual | 334.428959
16 20.9018099
-------------+-----------------------------Total | 1160688.04
19 61088.8441
Number of obs
F( 3,
16)
Prob > F
R-squared
Adj R-squared
Root MSE
=
20
=18506.73
= 0.0000
= 0.9997
= 0.9997
= 4.5718
-----------------------------------------------------------------------------y3 |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y2 |
1.939868
.5262442
3.69
0.002
.8242807
3.055456
x2 |
80.87406
9.530384
8.49
0.000
60.67055
101.0776
x5 |
5.069837
.687618
7.37
0.000
3.612152
6.527522
_cons | -8.792443
8.12776
-1.08
0.295
-26.02252
8.43764
-----------------------------------------------------------------------------Instrumented: y2
Instruments:
x2 x5 x3 x4
------------------------------------------------------------------------------
. * Estimación por el método de mínimos cuadrados
Bajo este método estimamos el sistema completo en un solo paso.
en tres etapas.
. reg3 (y1 y3 y2) (y2 y1 x2 x3 x4) (y3 y2 x2 x5)
Three-stage least-squares regression
---------------------------------------------------------------------Equation
Obs Parms
RMSE
"R-sq"
chi2
P
---------------------------------------------------------------------y1
20
2
16.32997
0.9945
3763.03
0.0000
y2
20
4
.9619987
0.9994
33824.52
0.0000
y3
20
3
4.366789
0.9997
69417.14
0.0000
--------------------------------------------------------------------------------------------------------------------------------------------------|
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y1
|
y3 |
2.446696
.2795843
8.75
0.000
1.898721
2.994671
y2 | -9.640954
1.751682
-5.50
0.000
-13.07419
-6.20772
_cons | -63.11623
25.76019
-2.45
0.014
-113.6053
-12.62718
-------------+---------------------------------------------------------------y2
|
y1 |
.1989394
.0022244
89.44
0.000
.1945796
.2032991
x2 | -3.747982
.322986
-11.60
0.000
-4.381023
-3.114941
x3 | -6.139365
.3045882
-20.16
0.000
-6.736347
-5.542384
x4 |
1.543914
.100502
15.36
0.000
1.346934
1.740895
_cons |
39.20859
.7726322
50.75
0.000
37.69425
40.72292
-------------+---------------------------------------------------------------y3
|
y2 |
2.223696
.3400349
6.54
0.000
1.55724
2.890152
x2 |
75.88808
6.292307
12.06
0.000
63.55539
88.22078
x5 |
4.666786
.4130684
11.30
0.000
3.857186
5.476385
_cons | -11.86901
6.277129
-1.89
0.059
-24.17195
.4339392
-----------------------------------------------------------------------------Endogenous variables: y1 y2 y3
Exogenous variables:
x2 x3 x4 x5
------------------------------------------------------------------------------
5
. * Otra manera de programar para estimar el sistema por mínimos cuadrados en tres etapas:
. global eq1 (y1 y3 y2)
. global eq2 (y2 y1 x2 x3 x4)
. global eq3 (y3 y2 x2 x5)
. reg3 $eq1 $eq2 $eq3
Three-stage least-squares regression
---------------------------------------------------------------------Equation
Obs Parms
RMSE
"R-sq"
chi2
P
---------------------------------------------------------------------y1
20
2
16.32997
0.9945
3763.03
0.0000
y2
20
4
.9619987
0.9994
33824.52
0.0000
y3
20
3
4.366789
0.9997
69417.14
0.0000
--------------------------------------------------------------------------------------------------------------------------------------------------|
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------y1
|
y3 |
2.446696
.2795843
8.75
0.000
1.898721
2.994671
y2 | -9.640954
1.751682
-5.50
0.000
-13.07419
-6.20772
_cons | -63.11623
25.76019
-2.45
0.014
-113.6053
-12.62718
-------------+---------------------------------------------------------------y2
|
y1 |
.1989394
.0022244
89.44
0.000
.1945796
.2032991
x2 | -3.747982
.322986
-11.60
0.000
-4.381023
-3.114941
x3 | -6.139365
.3045882
-20.16
0.000
-6.736347
-5.542384
x4 |
1.543914
.100502
15.36
0.000
1.346934
1.740895
_cons |
39.20859
.7726322
50.75
0.000
37.69425
40.72292
-------------+---------------------------------------------------------------y3
|
y2 |
2.223696
.3400349
6.54
0.000
1.55724
2.890152
x2 |
75.88808
6.292307
12.06
0.000
63.55539
88.22078
x5 |
4.666786
.4130684
11.30
0.000
3.857186
5.476385
_cons | -11.86901
6.277129
-1.89
0.059
-24.17195
.4339392
-----------------------------------------------------------------------------Endogenous variables: y1 y2 y3
Exogenous variables:
x2 x3 x4 x5
-----------------------------------------------------------------------------. * Compare los resultados de las estimaciones.
.
end of do-file
.
6