Dos dipolos elementales cruzados
Anuncio

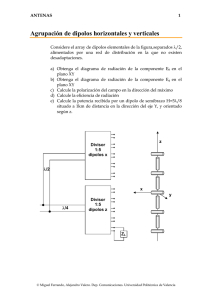
ANTENAS Problemas de antenas elementales 1 Dos dipolos elementales cruzados Dos dipolos elementales de longitud l=0.1λ se sitúan en posiciones ortogonales como muestra la figura. Los dipolos se alimentan con corrientes desfasadas 90º entre si. Obtener para dicha antena a) Los campos radiados en todo el espacio y el diagrama en los planos XY, YZ. Representar gráficamente los diagramas. b) La polarización en las direcciones (θ = 90º, φ = 90º), (θ = 45º, φ = 0º), (θ = 0º) c) La directividad d) La resistencia de radiación de cada dipolo aislado e) El campo transmitido a una distancia de 1 Km en la dirección del eje Y, cuando se alimentan los dos dipolos con corrientes de 1 A Z l/2 Y X © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS Problemas de antenas elementales Solución Vector de radiación El vector de radiación es la superposición de ambos dipolos G N = I x hxˆ + I y hyˆ = Ih ( xˆ + jyˆ ) En coordenadas esféricas es G Nθ = N ⋅θˆ = Ih ( xˆ + jyˆ ) ⋅ ( cos θ cos φ xˆ + cosθ sin φ yˆ − sin θ zˆ ) G Nφ = N ⋅ φˆ = Ih ( xˆ + jyˆ ) ⋅ ( − sin φ xˆ + cos φ yˆ ) Nθ = Ih cos θ ( cos φ + j sin φ ) Nφ = Ih ( − sin φ + j cos φ ) Campos radiados G µ e− jkr E = − jω Aθθˆ + Aφφˆ = − jω Nθθˆ + Nφ φˆ 4π r − jkr G µe E = − jω Ih ( cos φ + j sin φ ) cos θθˆ + jφˆ 4π r ( ) ( ( ) ) © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia 2 ANTENAS 3 Problemas de antenas elementales Diagramas de radiación PLANO XY θ= 120 P( φ ) 2 G µe E = − jω Ih ( cos φ + j sin φ ) jφˆ 4π r P (θ , φ ) = P0 − jkr ( ) 180 ( P( θ ) ) 90 2 60 30 1 0.5 180 0 0 210 330 240 PLANO YZ φ= 300 270 φ 1.5 150 G µe E = − jω Ih cos θθˆ + jφˆ 4π r P (θ , φ ) = P0 ( cos 2 θ + 1) 0 330 240 PLANO XZ − jkr 30 210 120 φ =0 60 0.8 0.6 0.4 0.2 0 150 π 90 300 270 θ z π 2 G µ e− jkr E = − jω Ih ( j ) cos θθˆ + jφˆ 4π r P (θ , φ ) = P0 ( cos 2 θ + 1) ( ) Polarización En el eje x, la radiación es la debida al dipolo del eje y, la polarización es lineal. En el eje y, la radiación es la debida al dipolo del eje x, la polarización es lineal. En general en el plano XY, la polarización es lineal. En el eje z, los campos se deben a la suma de los dos dipolos, con la misma amplitud y desfasados 90°, la polarización es circular En general, el campo tiene dos componentes, desfasadas 90° y de amplitud diferente, por lo tanto la polarización será elíptica. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS Problemas de antenas elementales G µ e− jkr E = − jω Ih ( cos φ + j sin φ ) cos θθˆ + jφˆ 4π r ( ) Directividad La directividad se puede calcular como D= 4π 1 2 ∫Ω 2 (1 + cos θ ) d Ω = 4π π 1 2π ∫ (1 + cos 2 θ ) sin θ dθ 2 0 = 1.5 Resistencia de radiación La resistencia de radiación de un dipolo elemental de longitud h es 2 ⎛h⎞ Rr = 80π ⎜ ⎟ = 80π 2 0.01 = 7.896Ω ⎝λ ⎠ 2 Campo radiado φ= π 2 ,θ = π 2 G µe kηe − jkr ˆ E =ω Ihφˆ = Ihφ 4π r 4π r 60π I E = I 0.1 = 6π = 18.85mv r r − jkr © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia 4