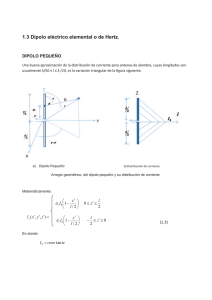
Agrupación de dipolos horizontales y verticales
Anuncio

ANTENAS 1 Agrupación de dipolos horizontales y verticales Considere el array de dipolos elementales de la figura,separados λ/2, alimentados por una red de distribución en la que no existen desadaptaciones. a) Obtenga el diagrama de radiación de la componente Eθ en el plano XY b) Obtenga el diagrama de radiación de la componente Eφ en el plano XY c) Calcule la polarización del campo en la dirección del máximo d) Calcule la eficiencia de radiación e) Calcule la potencia recibida por un dipolo de semibrazo H=5λ/8 situado a 1km de distancia en la dirección del eje Y, y orientado según z. z Divisor 1:5 dipolos x λ/2 x y λ/4 Divisor 1:5 dipolos z ZL © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 Solución Campos radiados El vector de radiación de la antena es ⎛ Ψz ⎞ ⎛ Ψz ⎞ sin 5 sin ⎜ ⎟ ⎜4 ⎟ G 2 ⎠ ⎝ ⎝ 2 ⎠ + I z hzˆ N = I x hxˆ Ψ Ψ sin z sin z 2 2 Ψ z = k z d = kd cosθ Los campos radiados se calculan a partir de las componentes esféricas del vector de radiación Eθ = − jω Eφ = jω µ e− jkr ( − sin θ N z + cosθ cos φ N x ) 4π r µ e− jkr N x sin φ 4π r Diagrama de radiación Eθ en el plano XY Eθ = − jω µ e− jkr ( − sin θ N z + cosθ cos φ N x ) 4π r µ e − jkr 4I zl Eθ = jω 4π r El campo es constante, el diagrama es omnidireccional en dicho plano Diagrama de radiación Eφ en el plano XY Eφ = jω µ e− jkr 5I x h sin φ 4π r Coincide con el diagrama de radiación de los dipolos orientados según x. El máximo de radiación está en la dirección del eje y © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 Polarización Las corrientes son iguales, pero hay un desfase de 900, debido a la diferencia de caminos de λ/2-λ/4 En la dirección del máximo, el campo es G µ e− jkr E = jω Il 4θˆ + 5 jφˆ 4π r ( ) La polarización es elíptica, con una relación axial de 5/4 Eficiencia La potencia total se reparte por igual entre todos los accesos, 9 de ellos están conectados a antenas, y 1 a una carga adaptada. La eficiencia es ηΩ = 9 = 0.9 10 Señal recibida a 1 km La longitud efectiva de un dipolo en la dirección del máximo es G λ 1 − cos kH l = zˆ π sin kH El campo recibido es G µ e− jkr E = jω Il 4θˆ + 5 jφˆ 4π r ( ) La señal recibida será G G 1 − cos kH 60e − jkr V = −E ⋅ l = j 4 Il sin kH r © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia