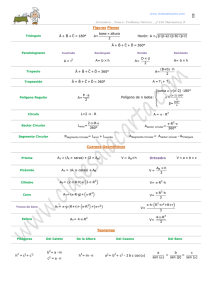
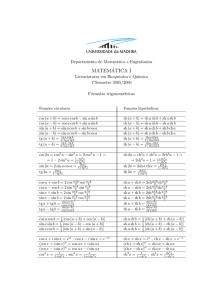
sen (+) cos (+) sen (+) cos (-) sen (-) cos (-) sen

www.clasesalacarta.com
1
Tema 4.- Trigonometría
Trigonometría
Estudio de los elementos de un triángulo
Ángulos
Cuando la longitud del arco coincida con la del radio, el ángulo formado vale 1 radián
360º  2 rad
180º   rad
Arco (r)
Ángulo
(radianes)
r
Grados
0
30
45
60
90
180
Radianes
0

6

4

3

2

cateto opuesto
Razones Trigonométricas



sen (+)
cos (-)
sen (+)
cos (+)
sen (-)
cos (-)
sen (-)
cos (+)
cateto contiguo
sen α =
Cateto Opuesto
Hipotenusa
cosec α =
cos α =
Cateto Contiguo
Hipotenusa
sec α =
Hipotenusa
1
=
Cateto Contiguo
cos α
cotg α =
Cateto Contiguo
cos α
=
Cateto Opuesto
sen α
tg α =
Cateto Opuesto
sen α
=
Cateto Contiguo
cos α
Hipotenusa
1
=
Cateto Opuesto
sen α
Ángulos Notables
0º
30º
45º
60º
90º
sen
0
1
2
2
2
3
2
1
cos
1
3
2
2
2
1
2
0
tg
0
1
3
1
3
+∞
Fórmula Fundamental
sen2 α + cos2 α = 1
1 + cotg2 α = cosec 2 α
tg2 α + 1 = sec 2 α
Bárbara Cánovas Conesa
Matemáticas _ B_ 4º ESO
Circunferencia Goniométrica
Circunferencia de radio 1 con centro en el origen (0,0)
y
sen α =
a
=a
1
cos α =
tg α =
b
=b
1
a
b
→ cosec α =
→ sec α =
→ cotg α =
1
a

b
1
b
a
b
a
Ángulos Opuestos
α + β = 0° (360°)
sen α = - sen β


cos α = cos β
tg α =
sen α
- sen β
=
= - tg β
cos α
cos β
Ángulos Complementarios
α + β = 90°


sen α = cos β
cos α = sen β
tg α = cotg β
Ángulos que difieren en 180º
β = 180° + α


sen β = - sen α
cos β = - cos α
tg β= tg α
Ángulos suplementarios
α + β = 180°


sen β = sen α
cos β = - cos α
tg β = - tg α
x
2