85 - licimep.org
Anuncio
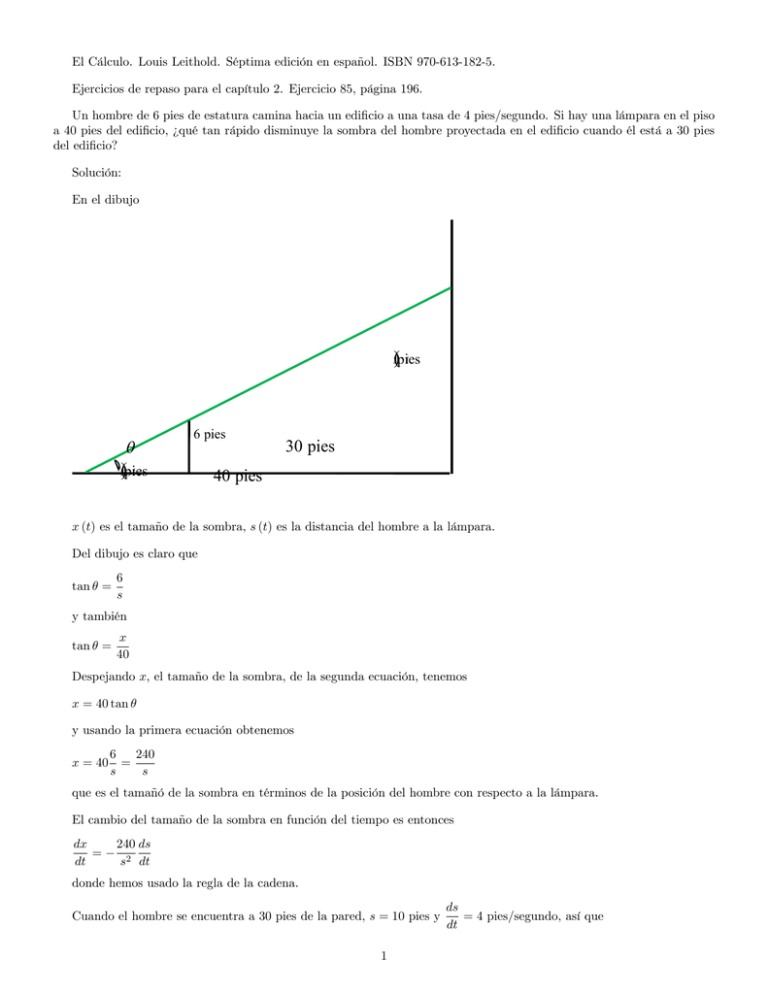
El Cálculo. Louis Leithold. Séptima edición en español. ISBN 970-613-182-5. Ejercicios de repaso para el capítulo 2. Ejercicio 85, página 196. Un hombre de 6 pies de estatura camina hacia un edi…cio a una tasa de 4 pies/segundo. Si hay una lámpara en el piso a 40 pies del edi…cio, ¿qué tan rápido disminuye la sombra del hombre proyectada en el edi…cio cuando él está a 30 pies del edi…cio? Solución: En el dibujo x()pies t θ 6 pies s()pies t 30 pies 40 pies x (t) es el tamaño de la sombra, s (t) es la distancia del hombre a la lámpara. Del dibujo es claro que tan = 6 s y también tan = x 40 Despejando x, el tamaño de la sombra, de la segunda ecuación, tenemos x = 40 tan y usando la primera ecuación obtenemos x = 40 6 240 = s s que es el tamañó de la sombra en términos de la posición del hombre con respecto a la lámpara. El cambio del tamaño de la sombra en función del tiempo es entonces dx = dt 240 ds s2 dt donde hemos usado la regla de la cadena. Cuando el hombre se encuentra a 30 pies de la pared, s = 10 pies y 1 ds = 4 pies/segundo, así que dt dx = dt 240 4= 102 48 = 5 9: 6 La sombra disminuye a una velocidad de 9.6 pies/segundo. 2








