En la vida cotidiana las rectas tangentes a una curva u objeto
Anuncio
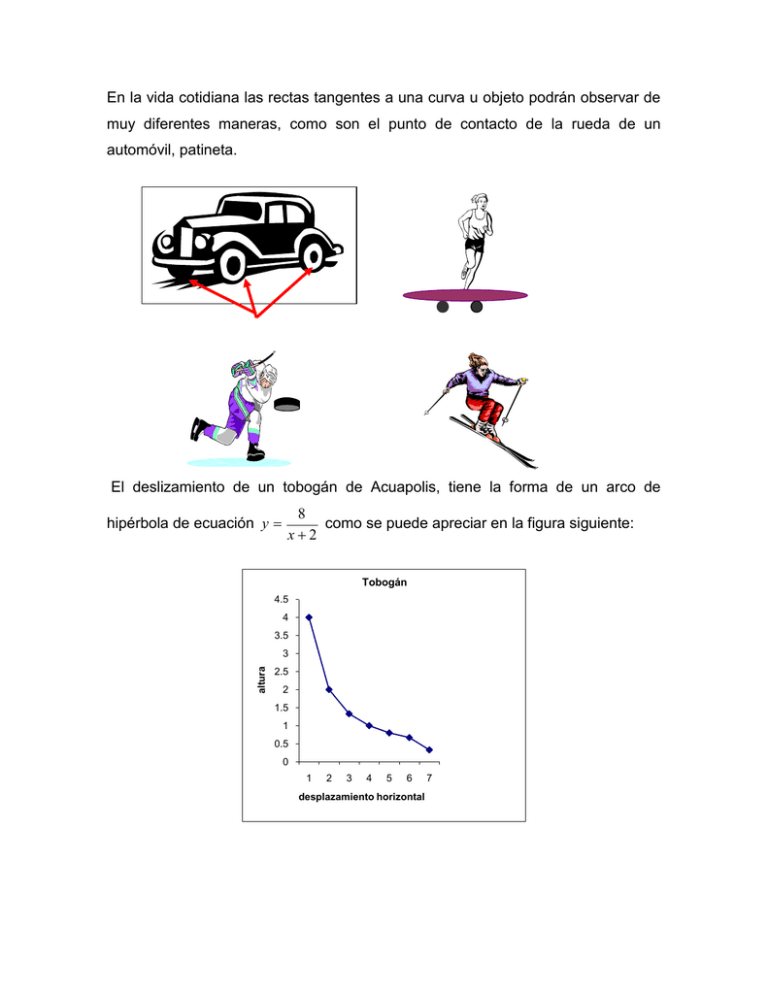
En la vida cotidiana las rectas tangentes a una curva u objeto podrán observar de muy diferentes maneras, como son el punto de contacto de la rueda de un automóvil, patineta. El deslizamiento de un tobogán de Acuapolis, tiene la forma de un arco de hipérbola de ecuación y 8 como se puede apreciar en la figura siguiente: x2 Tobogán 4.5 4 3.5 altura 3 2.5 2 1.5 1 0.5 0 1 2 3 4 5 6 desplazamiento horizontal 7 Calcula la pendiente del tobogán a los 3, 4, 5 y 6 m de la vertical del lanzamiento. Solución: en primer lugar se obtiene la derivada de la expresión, siendo: y, 8 ( x 2) 2 Para x = 3 resulta y , m3 8 25 Para x = 4 resulta y , m4 2 9 Para x = 5 resulta y , m5 8 49 Para x = 6 resulta y , m6 1 8 De acuerdo a los resultados de las pendientes, determina el ángulo de inclinación para cada caso: En base a los datos anteriores como explicarías la finalidad de este tipo de diseño, en relación a la velocidad de desplazamiento. Un cable de suspensión de un puente está sostenido por dos pilares (soportes) que distan 250 pies. Se considera que tiene una forma parabólica, con su punto más bajo de 50 pies por debajo de los puntos de suspensión. Hallar el ángulo entre el cable y el pilar. 250 pies 50 pies V(0,0) P(125,50) Solución: Considerando el vértice de la parábola en el origen de un sistema de coordenadas rectangulares y teniendo a la parábola que pasa por el punto P(125,50) se obtiene la ecuación de la parábola de y determina la derivada 2 x 2 . Posteriormente se 625 dy 4x que equivale a la pendiente. dx 625 En el punto del vértice (125 , 50 ), se substituye dando como resultado 4(125) 500 0.8 y el ángulo es 38o 40´´ por lo tanto el ángulo requerido es : 625 625 o 90 51o 20, 1.- Determinar las ecuaciones de la tangente y la normal de la expresión: y x 1 3 3 - x , para los puntos: A ( -1 , 0 ) B(2 ,3 ) C(3, 0 ) Se obtiene el valor de la derivada dy 8 - 4x dx 3 3 3 - x 2 La pendiente m que será válida resulta de sustituir el valor del punto 2 dy 8 - 4(-1) 3 dx 3 3 3 - (-1)2 2 Posteriormente se subtituyen los valores en la ecuación de la recta: ( y - y1 ) m ( x - x1 ) El punto A ( -1 , 0 ) resulta, ( y-0) 3 2 ( x - (-1) ) 2 ecuación de la tangente : y 3 4 ( x 1) Para la ecuación de la normal solo se substituye la pendiente inversa. ( y-0) 3 2 ( x - (-1) ) 2 ecuación de la normal : y - 3 2 ( x 1) 2 Realice para los dos puntos restantes el proceso anterior: Para el punto B ( 2, 3 ) Para el punto C ( 3, 0 ) CONCEPTO DE VELOCIDAD. Suponiendo que un objeto se mueve a lo largo de una línea recta de manera horizontal de acuerdo a la ecuación del movimiento s f (t ) donde (s) es el desplazamiento (distancia originada) del objeto respecto al origen, en el instante (t). La función f describe el movimiento, que se conoce como función de posición del objeto. En el intervalo ( t = a ) hasta ( t = a + h ) , el cambio de posición es f (a h) f (a) se representa dicho proceso a continuación. Posición a t t=a S f(a) f (a h) f (a) f(a+h) posición a t t(a+h) La velocidad promedio = desplazamiento f (a h) f (a) que es la secante. tiempo h Cuando calculamos la velocidad promedio sobre lapsos a, a h más y más cortos. En otras palabras, hagamos que la (h) tienda a cero. Se obtiene la derivada: V (a) límite f ( a h) f ( a ) Dando el significado que la velocidad en el instante h0 h t = a es igual a la pendiente de la recta tangente. Ejemplo: Se registraron las lecturas en °C cada hora a partir de la media noche, en el mes de diciembre en el valle de Toluca. El tiempo (x) se mide en horas a partir de la media noche. Como se muestra en la siguiente tabla. t (ºC) 6.5 6.1 5.6 4.9 4.2 4 4 4.8 6.1 8.3 10 12.1 14.3 16 17.3 18.2 18.8 17.6 16 14.1 11.5 10.2 9 7.9 7 GRAFICA DE TEMPERATURA TEMPERATURA EN ºC x(h) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 20 15 10 5 0 0 10 20 TIEMPO EN HORAS 30 a) Encuentre la razón promedio de cambio de la temperatura con respecto al tiempo: 1. Desde el medio día hasta las 3 PM. La temperatura cambia desde 14.3 hasta 18.2 º C T T (15) T (12) 18.2 14.3 3.9 en tanto que el cambio de tiempo es x 3 h Por consiguien te la ra`´on promedio de cambio de la temperatura con respecto al tiempo es 2. T 3.9 1.3 º C / h. x 3 Determina los siguientes intervalos tomando como ejemplo el inciso anterior. 3. Desde el medio día hasta las 2 PM. Sol. 1.5 ºC. 4. Desde el medio día hasta la 1 PM. Sol. 1.7 ºC. b) Estime la razón instantánea de cambio al mediodía. Como se observa en la gráfica de la tabla de valores. Se traza la tangente en el punto P donde x = 12 y después de medir los lados del triángulo ABC, estimamos que la pendiente de la recta es: BC 10.3 1.9 AC 5.5 Por lo tanto la razón instantánea de cambio de la temperatura con respecto al tiempo, al medio día es alrededor de 1.9 ºC / h.