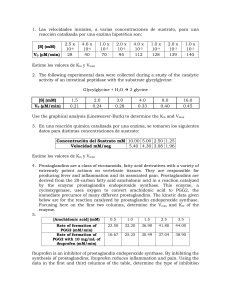
PROBLEMAS DE INHIBICIÓN 1. Se estudia la cinética de una

PROBLEMAS DE INHIBICIÓN
1.
Se estudia la cinética de una enzima en ausencia y presencia de un inhibidor A, a
una concentración 10 mM. La velocidad inicial viene dada en función de la
concentración de sustrato. Los datos obtenidos son:
[S] (mM)
1.25
1.67
2.50
5.00
10.00
V (mM min-1)
Sin inhibidor
Inhibidor A
1.72
0.98
2.04
1.17
2.63
1.47
3.33
1.96
4.17
2.38
a. Determina Vmax y KS en ausencia y presencia del inhibidor
b. ¿Qué tipo de inhibición se produce?
c. Calcula la constante de disociación (Ki) de la reacción de inhibición.
Solución:
Graficar 1/v versus 1[S]
1.2
1
y = 0.8582x + 0.3369
0.8
1/Vo
0.6
1/Vi
0.4
y = 0.4843x + 0.1951
0.2
0
0
0.2
0.4
Sin inhibición
1
1
Vmax = =
= 5.13mM / min
b 0.1951
K S = Vmax * (m ) = 5.13 * 0.4843 = 2.48mM
Con inhibición
1
1
app
V´max
= =
= 2.97 mM / min
b 0.3369
app
K Sapp = Vmax
* (m ) = 2.97 * 0.8582 = 2.55mM
Comaprando:
0.6
0.8
1
app
Vmax > Vmax
K S ≈ K Sapp
Por lo tanto es una INHIBICIÓN NO-COMPETITIVA
KI =
[I ]
Vmax
−1
app
Vmax
=
10mM
= 13.75mM
5.13mM / min
−1
2.97mM / min
2. En un experimento se midió la tasa inicial de una reacción enzimática, v, a varias
concentraciones de substrato [S]. La concentración de la enzima es 10 nM. Se graficó
1/v versus 1/[S] y se observó una línea recta en la cual el intercepto-y es 0.005 nM-1 seg
y la pendiente es 200 seg. ¿Cuál es el valor de KM y el de Vmax para esta reacción
enzimática? ¿Cuál es el valor de kcat para esta enzima? ¿Determine el coeficiente de
especificidad? 30 µM de un inhibidor, E, es adicionado y se observó que el interceptoy es 0.0065 nM-1 seg y la pendiente es 260 seg. ¿Qué tipo de inhibición se observó?
¿Cuál es el valor de Ki para el inhibidor con esta enzima?
Solución:
Se observa que se utilizó la ecuación de Lineweaver-Burk
1 KM 1
1
=
+
v Vmax [S ] Vmax
1/v
1/Vmax
Los datos del problema son:
m = 200 s
b = 0.005 s nM-1
KM/Vmax
-1/KM
1
= 200 ⋅ nM ⋅ s −1
0.005
K M = 200 ∗ Vmax = 200 ∗ 200 = 40,000 ⋅ nM
Sabemos que Vmax = kcat [E]t, por lo tanto
V
200 ⋅ nM ⋅ s −1
k cat = max =
= 20 ⋅ s −1
[E ]t
10 ⋅ nM
El coeficiente de especificidad es:
k
20 ⋅ s −1
α = cat =
= 0.0005 ⋅ s −1 nM −1
K M 40,000 ⋅ nM
En presencia del inhibidor tenemos
m = 260 s
b = 0.0065 s nM-1
Vmax =
1/[S]
1
= 153.846 ⋅ nM ⋅ s −1
0.0065
= 260 ∗ Vmax = 260 ∗ 153.846 = 40,000 ⋅ nM
app
Vmax
=
K Mapp
K M = K Mapp ,
Se observa que:
app
Vmax > Vmax
y
Por lo tanto se trata de una Inhibición no competitiva, entonces
app
Vmax
=
Vmax
 [I ] 
1 +

K i 

Despejando Ki
Ki =
[I ]
V max
app
V max
−1
=
30,000
= 100,000 ⋅ nM
200
−1
153.846
3. Para una reacción enzimática en presencia de un inhibidor competitivo, la
velocidad de reacción observada a una concentración de sustrato [S]i = 1.5 x 10-3 M es
igual a la velocidad de reacción sin el inhibidor a una concentración de sustrato [S]0 =
7.69 x 10-5 M. Calcule la constante de inhibición, Ki, del inhibidor si su concentración
[I] = 3.7 x 10-4 M.
Solución:
Para un inhibidor competitivo la relación [S]0 a [S]i para observar una misma velocidad es:
[S ]i = [S ]0 1 + [I ] 



Ki 
Despejando Ki
[I ]
3.7 x10 M
−5
[S ]i − 1 = 1.5x10 −3 M = 2x10 M
−1
[S ]0
7.69 x10 −5 M
−4
Ki =