Trigonometría: ejercicios resueltos

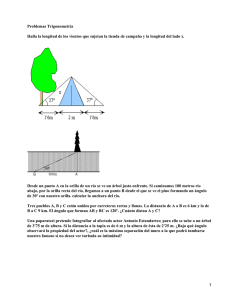
Cajón de Ciencias
Trigonometría: ejercicios resueltos
1) Resuelve los siguientes triángulos (halla todos los lados y ángulos que no se indican):
6
4
20º
30º
30º
16
9
2) A una determinada hora del día, un árbol arroja una sombra de 4 metros. A esa misma hora, un
hombre de 1,60m tiene una sombra de 2,4 metros. Calcula la altura del árbol.
3) Una escalera de 3 metros de altura está apoyada contra un muro formando un ángulo de 60º con
el suelo. Calcula la distancia que hay desde la base de la escalera hasta la pared.
4) Desde un avión que vuela a 1800 metros de altura se observa a lo lejos un pueblecito con un
ángulo de 30º. Calcula la distancia que hay entre el avión y el pueblo.
5) Los laterales de una tienda de campaña están sujetos al suelo con un ángulo de 40º. Si el ancho
de la tienda es de 3 metros, calcula la altura de la tienda de campaña.
40º
40º
3 metros
www.cajondeciencias.com
Cajón de Ciencias
Soluciones
1)
6
20º
En este primer triángulo lo más fácil es sacar los ángulos, porque sabemos que uno es un ángulo
recto y los tres deben sumar 180º:
70º
6
20º
90º
Luego podemos usar el seno de 20º para calcular la hipotenusa, y el coseno de 20º para el lado que
falta, aunque hay varios caminos válidos para llegar al mismo resultado:
sen 20º = 6/h
cos 20º = x/17,54
→
→
h = 6/sen20º = 17,54
x = 17,54·cos20º = 16,48
------
B
4
C
9
A
En este segundo triángulo, sacamos la hipotenusa mediante el Teorema de Pitágoras, y luego los
ángulos a través de las razones trigonométricas:
h2 = 42 + 92 → h2 = 97 → h = 9,85
cos A = 9/9,85 → cosA = 0,91 → A = 23,98º
cos B = 4/9,85 → cosB = 0,41 → B = 66,04
C = 90º
---
www.cajondeciencias.com
Cajón de Ciencias
30º
30º
16
Este triángulo no es rectángulo, pero es isósceles, así que lo partimos en dos triángulos iguales con
las siguientes medidas:
h
x
90º
30º
8
El ángulo que falta, por supuesto, valdrá 60º (el total debe sumar 180º). Por lo tanto, el ángulo
superior del triángulo del problema será de 120º.
Los dos lados que faltan se pueden sacar con razones trigonométricas o con Pitágoras.
cos 30º = 8/h →
sen 30º = x/9,24 →
h = 8/cos30º = 9,24
x = 9,24·sen30º = 4,62
2)
Es un problema de teorema de Tales, con dos triángulos semejantes: uno formado por el árbol y su
sombra y otro por el hombre y su sombra.
x
1,60
→
→
4
2,4
x = 1,60·4/2,4 = 2,66 m
3)
Ahora tenemos un triángulo formado por la escalera, el suelo y la pared. Conocemos el ángulo
escalera-suelo, y el ángulo pared-suelo es recto. La hipotenusa es la longitud de la escalera. Así que
nos basta usar el coseno para hallar la distancia de la escalera a la pared:
cos 60º = d/3
d = 3·cos 60º = 1,5m
www.cajondeciencias.com
Cajón de Ciencias
4)
El triángulo lo forman ahora el avión, el pueblo a lo lejos y el punto en el suelo que está justo
debajo del avión. Conocemos un ángulo y la distancia avión-suelo. Lo que tenemos que calcular es
la hipotenusa:
sen30º = 1800/h
h = 1800/sen30º = 3600m
5)
Igual que en el tercer triángulo del primer ejercicio, la tienda de campaña no forma un triángulo
rectángulo, pero podemos dividirla en dos triángulos iguales, con las siguientes medidas:
50º
h
90º
1,5m
40º
Usaremos la tangente para calcular directamente la altura:
tg 40º = h/1,5
h = tg 40º · 1,5 = 1,26m
www.cajondeciencias.com