Triángulos especiales
Anuncio

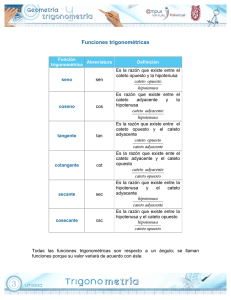
1 Unidad 1: Triángulo rectángulo 10 Tema 2: Triángulos especiales Lección 1: Triángulos especiales 10.12.0 Aplica las propiedades especiales d del triángulo recto. Triángulos especiales Existen dos tipos de triáng ángulos rectos especiales: 1.Los triángulos recttos isósceles (llamados triángulos 45º -45 45º -90º) 2. Los triángulos resulltantes después de cortar a la mitad un triángulo equilátero.. (llamados triángulos 30º -60º -90º) Teorema relacionad do con los triángulos 45º -45º 5º -90º Teorema del triángulo rrecto isósceles (45º -45º -90º) En un triángulo recto isósce eles, la longitud de la hipotenusa es 2 más larga que la longitud de cada cate eto o sea, es el resultado de la multiplica ación de la medida de uno de los dos ccatetos por 2 . a=b c= a 2 y c= b 2 ya que a=b. Por lo tanto, a 2 = b 2 por ser un triángulo isósceles Prof. S. Vélez, MA | 2011 2 Ejemplo 1: Si a= b= 7 unidades, entonces, ¿Cuánto mide la hipotenusa? c= a 2 c= 7 2 Ejemplo 2: Si a=4 unidades, entonces, ¿Cuánto mide e l o t r o c a t e t o y la hipotenusa? a=b=4 c= a 2 c= 4 2 Ejemplo 3: Si un cateto mide 3, la hipotenusa mide ______. c= a 2 c= 3 2 Prof. S. Vélez, MA | 2011 3 Ejemplo 4: Si la hipotenusa mide 3 6 , los catetos medirán ______. 3 6 = 3 3 2 Ejemplo 5: Si la hipotenusa mide 7 10 , los catetos medirán ______. 7 10 = 7 5 2 Prof. S. Vélez, MA | 2011 4 Teorema relacionado con los triángulos 30º -60º -90º. En un triángulos 30º -60º -90º la medida de la hipotenusa es dos veces mayor que la medida del cateto de menor longitud, y la longitud del cateto mayor es 3 más grande que la longitud del cateto menor. Suponga que a < b, entonces; c= 2a b=a 3 Ejemplo 1: Si la hipotenusa mide 100 , el cateto corto medirá ______. c= 2a 100= 2a 100= 2∙a a= 100 = 50 2 Prof. S. Vélez, MA | 2011 5 Ejemplo 2: Si la hipotenusa mide 48 , el cateto corto medirá ______. c= 2a 48= 2a 48= 2∙a a= 48 = 24 2 Ejemplo 3: Si el cateto corto mide 21, la hipotenusa medirá ____. c= 2∙21 c= 42 Prof. S. Vélez, MA | 2011 6 Ejemplo 4: Si el cateto corto mide 36, la hipotenusa medirá ____. c= 2∙36 c= 72 Ejemplo 5: Si el cateto corto mide 36, el cateto largo medirá ____. b= a∙ 3 b= 36 ∙ 3 b= 36 3 Prof. S. Vélez, MA | 2011 7 Ejemplo 6: Si el cateto corto mide 8, el cateto largo medirá ____. b= a∙ 3 b= 8 ∙ 3 b= 8 3 Ejemplo 7: Si el cateto largo mide 10 3 , el cateto corto medirá ____. b= a∙ 3 10 3 = a ∙ 3 10= a Prof. S. Vélez, MA | 2011