UNIDAD 7 Vectores
Anuncio
UNIDAD 7 Vectores
4. Resoluciones de la autoevaluación del libro de texto
1
8
8
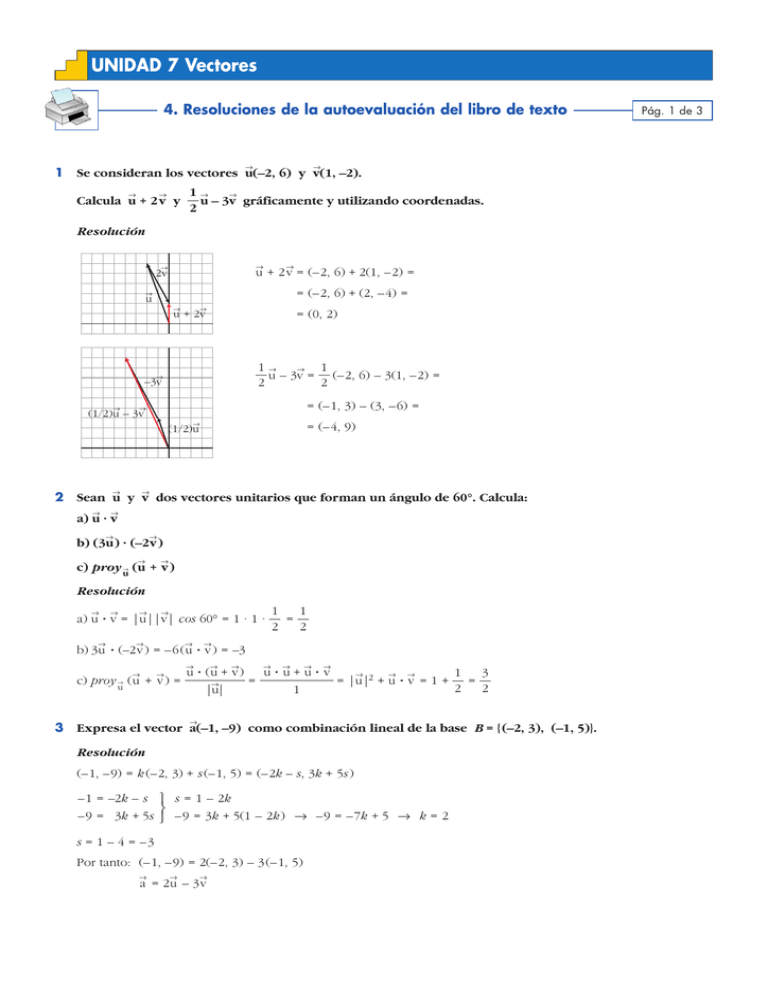
Se consideran los vectores u(–2, 6) y v(1, –2).
8
8
Calcula u + 2 v y
18
8
u – 3v gráficamente y utilizando coordenadas.
2
Resolución
8
8
8
u + 2 v = (–2, 6) + 2(1, –2) =
2v
= (–2, 6) + (2, –4) =
8
u
8
8
= (0, 2)
u + 2v
18
1
8
u – 3v = (–2, 6) – 3(1, –2) =
2
2
8
–3v
8
= (–1, 3) – (3, –6) =
8
(1/2)u – 3v
8
= (–4, 9)
(1/2)u
2
8
8
Sean u y v dos vectores unitarios que forman un ángulo de 60°. Calcula:
8
8
a) u · v
8
8
b) (3u ) · (–2 v )
8
8
c) proy u8 (u + v )
Resolución
8
8
8
8
a) u · v = |u||v| cos 60° = 1 · 1 ·
8
8
8
1
1
=
2
2
8
b) 3 u · (–2 v ) = –6( u · v ) = –3
8
8
8
8
8
8
8
u · ( u + v)
u· u+u· v
1
3
8 8
8
c) proy 8u ( u + v ) =
=
= |u|2 + u · v = 1 +
=
8
2
2
|u|
1
8
3
8
8
Expresa el vector a(–1, –9) como combinación lineal de la base B = { (–2, 3), (–1, 5)}.
Resolución
(–1, –9) = k (–2, 3) + s (–1, 5) = (–2k – s, 3k + 5s )
–1 = –2k – s ° s = 1 – 2k
¢
–9 = 3k + 5s £ –9 = 3k + 5(1 – 2k ) 8 –9 = –7k + 5 8 k = 2
s = 1 – 4 = –3
Por tanto: (–1, –9) = 2(–2, 3) – 3(–1, 5)
8
8
8
a = 2u – 3 v
Pág. 1 de 3
UNIDAD 7 Vectores
4. Resoluciones de la autoevaluación del libro de texto
4
8
8
Consideramos los vectores u (0, 2) y v (1, √3 ). Calcula:
a) Su producto escalar.
b) El módulo de ambos vectores.
c) El ángulo que forman.
Resolución
8
8
a) u · v = (0, 2) · (1, √3 ) = 0 · 1 + 2 · √3 = 2√3
8
b) | u | = √02 + 22 = 2
8
|v | =
—
√12 + √3 2
8
ì
8 8
c) cos ( u, v ) =
8
u·v
2 √3
√3
=
=
8
8
2
|u| ·| v| 2 · 2
( )
ì
√3
8 8
( u, v ) = arc cos
5
=2
2
= 30°
8
Sea u(–3, k), calcula k de forma que:
8
8
a) u sea ortogonal a v(4, – 6).
8
b) El módulo de u sea igual a 5.
Resolución
a) El producto escalar de dos vectores ortogonales es igual a 0.
8
8
8
8
u2v ï u·v =0
8
8
u · v = (–3, k ) · (4, –6) = –12 – 6k = 0 8 k = –2
8
b) | u | = √9 + k 2 = 5 8 9 + k 2 = 25 8 k = ±4
6
8
8
Determina las coordenadas de un vector a (x, y) que forme con el vector v (–1, 0) un
ángulo de 60° y cuyo módulo sea 2.
Resolución
ì
8 8
cos ( a, v ) = cos 60° =
8
8
a·v
1
–x
= 8 8 =
8 x = –1
2
2·1
|a| ·| v|
8
| a | = √x 2 + y 2 = √1 + y 2 = 2 8 1 + y 2 = 4 8 y 2 = 3 8 y = ± √3
8
—
° a (–1, √ 3 )
—
Hay dos soluciones para el vector a : ¢ 8
£ a (–1, –√ 3 )
8
Pág. 2 de 3
UNIDAD 7 Vectores
4. Resoluciones de la autoevaluación del libro de texto
7
8
8
8
Obtén un vector u(x, y) ortogonal a v(8, 6) y cuyo módulo sea la mitad del de v.
Resolución
8
8
8
8
u2v ï u·v =0
8
8
| u | = √x 2 + y 2
| v | = √64 + 36 = 10
(x, y) · (8, 6) = 8x + 6y = 0
1 8
| v | 8 √x 2 + y 2 = 5 8 x 2 + y 2 = 25
2
8
|u | =
Resolvemos el sistema:
3
–—
8x + 6y = 0 ° x = 4 y
¢
25
x 2 + y 2 = 25 £ 9 2
— y + y 2 = 25 8 — y 2 = 25 8 y 2 = 16 8 y = ±4
16
16
y = 4 8 x = –3
y = –4 8 x = 3
8
8
8
Hay dos soluciones para u : u (–3, 4); u (3, –4)
8
8
8
8
8
Calcula la proyección de v sobre u, siendo u(2, 0) y v(–3, –1).
Resolución
8
8
proy 8u v =
9
Pág. 3 de 3
8
8
u·v
–6 + 0
=
= –3
8
2
|u|
8
Sean a y b dos vectores unitarios que forman un ángulo de 120°.
8
8
8
8
Calcula |a + b| y |a – b|.
Resolución
8
8
8
8
8
8
8
8
8
8
8
8
8
8
| a + b |2 = ( a + b ) · ( a + b ) = a · a + 2 a · b + b · b =
8
ì
( )
8
8 8
= | a |2 + 2| a || b | cos ( a, b ) + | b |2 = 1 + 2 · –
1
+1=
2
8
8
= 1 – 1 + 1 = 1 8 | a + b| = 1
8
8
8
8
8
8
8
8
8
8
8
8
8
8
| a – b |2 = ( a – b ) · ( a – b ) = a · a – 2 a · b + b · b =
8
ì
8 8
8
( )
= | a |2 – 2| a || b | cos ( a, b ) + | b |2 = 1 – 2 · –
8
8
= 1 + 1 + 1 = 3 8 | a – b | = √3
1
+1=
2