Ejercicios INDIVIDUALES puntuables, bloque 2, RESUELTOS
Anuncio

TECNOLOGÍA DE COMPUTADORES / SISTEMAS DIGITALES.
SEGUNDO EJERCICIO INDIVIDUAL PUNTUABLE. GRUPOS DE MAÑANA.
18 de noviembre de 2009
SOLUCIÓN
1) Dado un número de 1 dígito expresado en BCD, diseñe un circuito que detecte si
dicho número es primo (considere que el 0 no es primo). Utilice un multiplexor
controlado por los dos bits menos significativos del dígito en cuestión. (0,1 puntos).
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
F(A,B,0,0) = 0
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
F(A,B,0,1) = A’
0
0
A
1
B
2
1
3
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Primo
0
1
1
1
0
1
0
1
0
0
X
X
X
X
X
X
F(A,B,1,0) = B’
F(A,B,1,1) =1
Primo
MUX
1
0
C
D
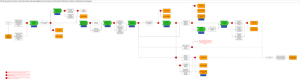
2) Dado el circuito lógico de la figura:
a) Escribir la función lógica (0,05 puntos).
F = {[(b xor (a’b)’)] * [(ab) xor a xor b)]}’
b) Simplificar e indicar la función lógica que realiza (0,05 puntos).
Implementa una XNOR.
3) Diseñar un generador de paridad para 4 bits (A3, A2, A1, A0) mediante un
decodificador 4x16 activo a nivel alto. La salida del generador de paridad toma el valor
“1” cuando el número de bits a “1” en los 4 bits de entrada es impar. (0,1 puntos).
A3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
A2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
A0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
P
0
1
1
0
1
0
0
1
1
0
0
1
0
1
1
0
A3
3
A2
2
A1
1
A0
0
DEC
4x16
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
P
TECNOLOGÍA DE COMPUTADORES / SISTEMAS DIGITALES.
SEGUNDO EJERCICIO INDIVIDUAL PUNTUABLE. GRUPOS DE TARDE.
18 de noviembre de 2009
SOLUCIÓN
1) Un sistema utiliza 4 bits (C3 C2 C1 C0) para codificar las 10 primeras letras del
alfabeto. Se trata de diseñar un circuito que sea capaz de detectar si un determinado
código corresponde a una vocal. Utilice un multiplexor controlado por los bits C2C1.
(0,1 puntos).
a
b
c
d
e
f
g
h
i
j
-
F(C3,0,0,C0) = C0’
C3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
C2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
F(C3,0,1,C0) = 0
C0
0
0
1
C0
2
0
3
C1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
C2
Vocal
1
0
0
0
1
0
0
0
1
0
X
X
X
X
X
X
F(C3,1,0,C0) = C0’
F(C3,1,1,C0) = 0
Vocal
MUX
1
C0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
C1
2) Dado el circuito lógico de la figura:
a) Escribir la función lógica (0,05 puntos).
F = {[(a' xor b)*b]' }xor{ [(a xor b)*(ab)]'}
b) Escribir la tabla de verdad e indicar la función lógica que realiza (0,05 puntos).
A
0
0
1
1
B (A’ xor B)
0
1
1
0
0
0
1
1
(b * (a’ xor b))’
1
1
1
0
ab
0
0
0
1
A xor b
0
1
1
0
((ab) * (a xor b))'
1
1
1
1
F
0
0
0
1
Implementa una AND.
3) Diseñar un generador de paridad impar para 4 bits (A3, A2, A1, A0) mediante un
decodificador 4x16 activo a nivel bajo y puertas lógicas. La salida del generador de
paridad impar toma el valor “1” cuando el número de bits a “1” en los 4 bits de entrada
es par. (0,1 puntos).
A3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
A2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
A0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
I
1
0
0
1
0
1
1
0
0
1
1
0
1
0
0
1