TEMA 9 Electrostática

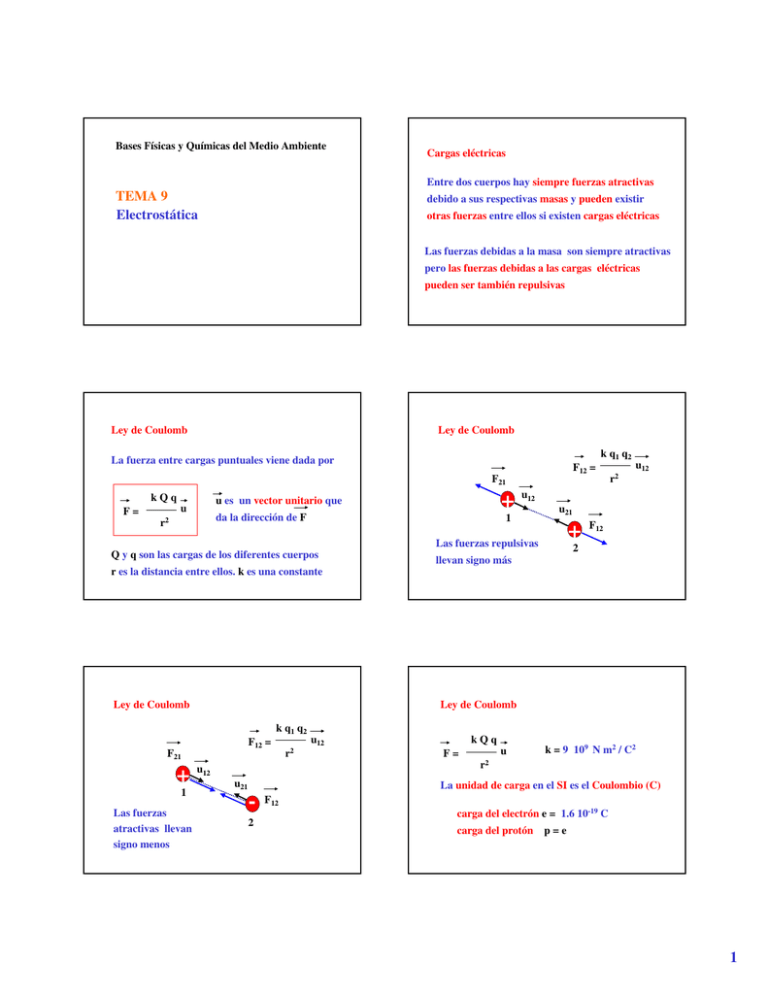
Bases Físicas y Químicas del Medio Ambiente
Cargas eléctricas
Entre dos cuerpos hay siempre fuerzas atractivas
TEMA 9
Electrostática
debido a sus respectivas masas y pueden existir
otras fuerzas entre ellos si existen cargas eléctricas
Las fuerzas debidas a la masa son siempre atractivas
pero las fuerzas debidas a las cargas eléctricas
pueden ser también repulsivas
Ley de Coulomb
Ley de Coulomb
La fuerza entre cargas puntuales viene dada por
F12 =
F21
F=
kQq
da la dirección de F
r2
r es la distancia entre ellos. k es una constante
Ley de Coulomb
Las fuerzas
atractivas llevan
signo menos
r2
u12
u21
+
Las fuerzas repulsivas
F12
2
llevan signo más
Ley de Coulomb
F12 =
F21
1
u12
1
Q y q son las cargas de los diferentes cuerpos
+
+
u es un vector unitario que
u
k q1 q2
u12
u21
2
k q1 q2
r2
u12
F=
kQq
u
k = 9 109 N m2 / C2
r2
La unidad de carga en el SI es el Coulombio (C)
F12
carga del electrón e = 1.6 10-19 C
carga del protón p = e
1
Campo eléctrico
Comparación con la ley de Newton
GMm
F=
r2
G = 6.67 10-11 N m2 / kg2
u
fuerza sobre las posibles cargas presentes dada
por la ley de Coulomb. Crea por tanto un campo
masa del electrón me = 9.11 10-28 kg
masa del protón mp = 1.67
de fuerzas
10-27 kg
El campo eléctrico es la fuerza que la carga
La fuerza entre cargas es mucho mayor que
la que hay entre masas
Campo eléctrico
carga creadora del campo
kQ
E=
r2
u
vector unitario
en la dirección
desde la carga al
punto donde se mide
el campo
vector campo
eléctrico
distancia de la
carga creadora
del campo al
punto donde se mide
creadora del campo ejercería sobre la unidad de
carga positiva
Campo eléctrico
P
+
E
+
E
u
la dirección del campo
es radial
Campo eléctrico
Campo eléctrico
P
-
E
-
Una carga en un punto del espacio ejerce una
E
El campo eléctrico total en un punto es la suma
vectorial de los campos creados por todas las
cargas presentes
E1
u
E2
la dirección del campo
es radial
E2
ET
2
Campo eléctrico creado por dos cargas positivas
E
E2
E1
+
Los cam pos
se sum an en
cada punto
+
E1
E2
+
E
Campo eléctrico en dos cargas de distinto signo
Los cam pos
se sum an en
cada punto
+
-
-
Campo eléctrico creado por una placa cargada
E=
+
+
Campo eléctrico creado por dos cargas diferentes
---
Campo eléctrico generado por dos cargas del
mismo signo
Si la placa es
E
infinita, E
no depende
de la distancia
a la placa
σ
σ es la densidad superficial
2 εo
de carga
Campo eléctrico creado por una placa cargada
+
++
+
+
+
+
+
E
k = 1/ 4 π εo = 9 109 N m2 / C2
εo = 8.85 10-12 C2 / N / m2
E=
σ
2 εo
permitividad
eléctrica en el
vacío
(carga por unidad de S)
3
Campo eléctrico creado por una placa cargada
+
+
Las fuerzas eléctricas son conservativas. Esto
E
E
E
implica que pueden derivarse de un potencial
E
Campo en un punto
lejano de la placa
Potencial eléctrico
Una carga crea un
campo escalar de
potenciales a su
alrededor
Potencial eléctrico
∇V
E = -∇
V=kQ/r
El potencial creado por una carga es un escalar
Energía potencial eléctrica
-
U=qV=
kQq
r
superficies equipotenciales
F=- ∇U=qE
El potencial creado por varias cargas en un punto
es la suma de los potenciales creados por las cargas
individuales
La fuerza de Coulomb es el gradiente de la energía
potencial eléctrica
Unidades
Dipolos eléctricos
La fuerza de Coulomb se mide en el SI en N
Un par de cargas iguales q y de signo contrario
El potencial se mide en el SI en voltios (V)
situadas a una distancia fija d constituye un dipolo
eléctrico
El campo eléctrico se mide en el SI en N/C o V/m
La energía potencial se mide en el SI en J
d
-
+
q
ET
q
4
Dipolos eléctricos
Dipolos eléctricos
r
d
-
+
q
Puede definirse el vector momento dipolar como
ET
µ=qd
µ es un vector que es paralelo a d y que va en la
q
dirección de la carga positiva a la negativa
El campo creado a distancias r lejanas del dipolo
es proporcional a 1/ r3
µ se mide en Debyes (D). 1 D = 3.30 10-30 C m
Dipolos eléctricos
Dipolos eléctricos
La energía potencial eléctrica de un dipolo
Las moléculas formadas por átomos diferentes
dentro de un campo eléctrico E es
también poseen momentos dipolares
-
U = µ E = | µ | | E | cos θ
q
Ejemplo: molécula de HCl
El dipolo se mueve
θ
hasta que cos θ = - 1
+q
y la energía es
E
mínima
Parte de los electrones del enlace se comparten
H
Cl
Conductores
formando un enlace covalente y parte quedan en
Cuando los electrones de muchos átomos se
alrededor del átomo de Cl ⇒ hay un exceso de
mueven libremente a través del sólido tenemos un
carga negativa en el Cl y un defecto en el H
conductor
d
δ q-
|µ| =δqd
δ q+
µ
los µ moleculares
son del orden
de 1-5 D
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
iones positivos
fijos
gas de electrones
5
Conductores
Conductores
- --- - - -- -- -
E
E
- --- - - -- -- -
E
En presencia de un campo eléctrico los electrones
predominio
cargas -
se mueven libremente pero los iones no
Conductores
E
E
predominio
cargas +
Aislantes o dieléctricos
EINTERIOR
- --- - - - -- -- -
EINTERIOR
La suma de
los campos
interior y
exterior
E
En ellos los electrones no pueden moverse
libremente. Normalmente están próximos a su
molécula correspondiente
en el conductor
iones positivos
es cero
EEXTERIOR
electrones
Los conductores hacen de escudos para la radiación
Dentro de un conductor ETOTAL = 0
Aislantes o dieléctricos
Aislantes o dieléctricos
En presencia de un campo eléctrico las moléculas
---
---
se polarizan ⇒ se forma un dipolo inducido
---
-----
E
µ=αE
--
polarizabilidad de
µ
la molécula
E
---
E
EINTERNO
El campo interno es menor que en el caso de un
conductor ETOTAL ≠ 0
6
Condensadores
Condensadores
El conjunto de dos placas infinitas paralelas con
La diferencia
cargas opuestas es un condensador
E(-)
E(+)
+
++
+
+
+
+
+
---
E(-)
Fuera del
condensador
E=0
E=0
dentro del
E(+)
condensador
de potencial
-- E = 0
--
eléctrico dentro
del condensador
es
∆ V= E d = σ d / εo
d
|E|| = σ / εo
Condensadores
+
++
+
+
+
+
+
Condensadores
Eefectivo = E εo / ε
Si en lugar del
vacío metemos
constante dielectrica
del medio
un dieléctrico en
E= 0
E=0
el interior del
condensador
E= 0
E=0
reduce el campo en
E y V cambian
d
∆ V= Eefectivo d = σ d / ε
Un dieléctrico
el interior con respecto
d
al vacío un factor εo / ε
Condensadores
Condensadores
Un condensador se define mediante una
En el caso de un dieléctrico
propiedad denominada capacidad
La capacidad es el cociente entre la carga
almacenada y el potencial en su interior
C = Q / ∆V = σ S / ∆ V = ε S / d
C = Q / ∆ V (εε / εo)
La capacidad de un condensador aumenta
al introducir un dieléctrico
La unidad de capacidad en el SI es el Faradio
(F). Un condensador típico tiene C ≈ 1 µ F
7
Condensadores
El condensador puede almacenar una energía
dada por
U = 1/2 C ∆ V2 = 1/2 Q2 / C
Los condensadores son componentes corrientes
de los circuitos eléctricos
Una membrana celular se puede describir de
forma simple mediante un condensador
8