Capacidad y dieléctricos
Anuncio

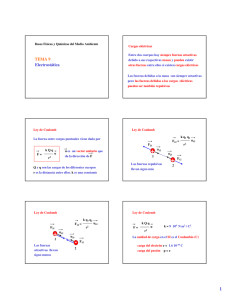
Capacidad y dieléctricos Almacenamiento de carga y energía electrostática Esquema 1. CAPACIDAD Y CONDENSADORES 2. ALMACENAMIENTO DE ENERGÍA ELÉCTRICA 3. COMBINACIÓN DE CONDENSADORES 4. POLARIZACIÓN. 5. CARGA LIBRE Y CARGA LIGADA. 6. VECTOR DESPLAZAMIENTO ELÉCTRICO. TEOREMA DE GAUSS. 7. CAPACIDAD Y DIELÉCTRICOS. 1. Capacidad y condensadores Condensador : dispositivo que almacena carga y energía eléctrica. Capacidad del condensador Æ cociente entre carga y voltaje. Q C= V UnidadÆ El Faradio [F ] = [C V ] La capacidad depende de la forma, el tamaño y el material del que esta hecho el condensador. 1.2 Ejemplos de condensadoresPlacas paralelas +Q E -Q Diferencia de potencial Entre las placas Aε 0 C= d σ E= ε0 d V = V + −V − = E d = Capacidad Campo entre las placas σ d Qd = ε0 Aε 0 Superficie de las placas Permitividad del vacío 1.2 Ejemplos de condensadoresCondensador esférico +Q E -Q R r E= ra rb C = 4πε 0 rb − ra 4πε 0 r 2 rˆ Campo entre las placas Q 1 1 − V = V −V = 4πε 0 ra rb + Diferencia de potencial Entre las placas Q Capacidad − Radio interior Radio exterior 2. Almacenamiento de energía eléctrica Energía potencial eléctrica almacenada en el condensador = trabajo realizado para cargarlo. Q dU = V ⋅ dQ = C ⋅ dQ Q 1 Q2 1 1 Q U = ∫ ⋅ dQ = = CV 2 = QV 2 C 2 2 C 0 Descarga del condensador Æ se recupera la energía como trabajo realizado por las fuerzas eléctricas. El condensador almacena carga y energía. 2.1 Densidad de energía eléctrica en el vacío Ejemplo: condensador plano Æ Resultado general. Densidad de energíaÆ Energía eléctrica por unidad de volumen. dU QV +Q E u= d -Q Vol = Ad 1 U = QV 2 Volumen Energía dVol = 1 u = ε0E2 2 2 Ad 3. Combinación de condensadores PARALELO Vb C2 Va SERIE C1 V = Vb − Va Q = Q1 + Q2 = C1V + C2V Q = (C1 + C2 )V = CeqV Ceq = C1 + C2 N condensadores Ceq = C1 + K + C N Va Vb C1 Vc C2 Vc − Va = Vc − Vb + Vb − Va Q Q Q = + Ceq C1 C2 1 1 1 = + Ceq C1 C2 N condensadores 1 1 1 = +L+ Ceq C1 CN 4.1 Polarización. Dipolos inducidos y orientación. Un campo eléctrico externo Induce momentos dipolares E F F F p F + -- + Orienta dipolos ya existentes r r U = −p⋅E La energía es mínima en la dirección del campo eléctrico Æ el dipolo se orienta. 4.2 Vector polarización. Una porción de material no conductor se polariza al aplicar un campo E externo + + - - ++ -+ - +- +- + + + + +-- - +- - + + - +- +- +- - Las moléculas y átomos se convierten en pequeños dipolos Vector polarización r r P = np Nº dipolos por volumen Momento dipolar La polarización es proporcional al campo aplicado Susceptibilidad eléctrica r r P = χ eε 0 E [ r −2 P = Cm ] Unidades 5. Carga libre y carga ligada PN = σ p σ total EN = ε0 σ p = χ eσ total E + + + + + Densidad de carga libre σl P - Densidad de carga de polarización + + + + - - - - Componentes normales ( perp. a las superficies) de los vectores. σp σ total = σ l − σ p Carga ligada a átomos y moléculas 6.1 Vector Desplazamiento D eléctrico σ l = σ total + σ p DN = ε 0 E N + PN r r r D = ε0E + P r r r r D = ε 0 E + ε 0 χe E = ε E ε 0 (1 + χ e ) = ε (1 + χ e ) = ε r + + + + + Densidad de P - Densidad de carga de polarización + + + + - - - - Relacionado con la carga libre E carga libre σl σl σp σ total = σ l − σ p Permitividad del medio Permitividad relativa σ l = ε r σ total 6.2 Ley de Gauss general El flujo del vector Desplazamiento eléctrico a través de una superficie cerrada es igual a la carga libre encerrada en su interior. r r libre Φ = ∫ D ⋅ dA = Qenc. libre total r r Qenc Qenc. . Φ = ∫ E ⋅ dA = = ε ε0 La ley de Gauss simplifica los cálculos de campo eléctrico en casos de gran simetría. La superficie gaussiana no es una superficie real ( es matemática). 7. Capacidad y dieléctricos E El campo E Er = r E0 εr La diferencia de potencial V = V0 + + + + + Densidad de carga libre σl εr Aumenta la capacidad C = ε r C0 + + + + - - - - Se reducen σ total Carga con dieléctrico P - Densidad de carga de polarización σp σl = εr Carga sin dieléctrico