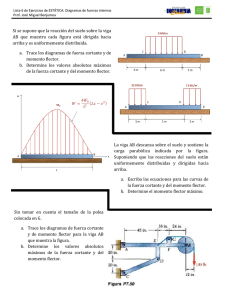
Calcular el esfuerzo cortante máximo, el momento flector máximo y

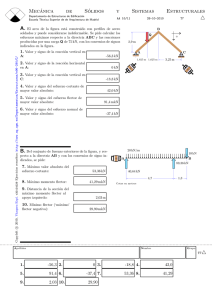
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Calcular el esfuerzo cortante máximo, el momento flector máximo y la
máxima deformación del siguiente supuesto, dejando este último valor en
función de E⋅I.
6T
4 T/m
B
A
2m
4m
Para resolver el problema utilizaremos la superposición de los siguientes
casos simples:
4 T/m
[1]
B
A
6m
+
6T
[2]
A
B
C
2m
4m
1
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
De la situación [1] obtenemos en el Prontuario las expresiones que
determinan el momento flector, el esfuerzo cortante y la ecuación de la elástica:
M=
4⋅x
q⋅ x
⋅ (l − x ) =
⋅ (6 − x ) = 12 ⋅ x − 2 ⋅ x 2
2
2
6

l

Q = q ⋅  − x  = 4 ⋅  − x  = 12 − 4 ⋅ x
2

2

(
)
(
yx =
4⋅x
q⋅ x
⋅ x 3 − 2 ⋅ l ⋅ x 2 + l3 =
⋅ x3 − 2 ⋅ 6 ⋅ x2 + 63
24 ⋅ E ⋅ I
24 ⋅ E ⋅ I
yx =
x
⋅ x 3 − 12 ⋅ x 2 + 216
6 ⋅E ⋅I
(
)
)
Del mismo modo, en el Prontuario obtenemos las expresiones del
momento flector, esfuerzo cortante y deformada del supuesto [2]:
M AC =
P ⋅b
6⋅4
⋅x =
⋅x = 4⋅x
l
6
MCB =
P⋅a
6⋅2
⋅ (l − x ) =
⋅ (6 − x ) = 12 − 2 ⋅ x
l
6
Q AC =
P⋅b 6 ⋅ 4
=
= 4T
l
6
Q CB = −
P ⋅a
6⋅2
=−
= −2T
l
6
y AC
P ⋅ l ⋅ b ⋅ x  b 2 x2  6 ⋅ 6 ⋅ 4 ⋅ x  42 x 2 
2⋅x
⋅ 20 − x 2
=
⋅  1 − 2 − 2  =
⋅ 1 − 2 − 2  =
6 ⋅E ⋅I 
6 ⋅E ⋅I  6
l
l 
6  3 ⋅E ⋅I
y CB
2
2
P ⋅ l ⋅ a ⋅ (l − x )  a 2  l − x   6 ⋅ 6 ⋅ 2 ⋅ (6 − x )  2 2  6 − x  
=
⋅ 1 − 2 − 
⋅ 1 − 2 − 
 =
 
6 ⋅E ⋅I
6 ⋅E ⋅I
l
 l  
 6  

 6
(
)
2
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
y CB =
2
6 ⋅ 6 ⋅ 2 ⋅ (6 − x )  6 2 − 2 2 − (6 − x )  (6 − x )
⋅
⋅ − 4 − x 2 + 12 ⋅ x
=
2
6 ⋅E ⋅I
6

 3 ⋅E ⋅I
[
]
7Obtención del momento flector máximo
Sumamos las expresiones obtenidas en ambos casos, teniendo en
cuenta la existencia de dos tramos, uno desde el apoyo dorsal hasta el punto
de aplicación de la carga puntual (tramo AC) y otro desde este punto hasta el
apoyo frontal (tramo CB).
M AC = M[1] + M[2 ]AC = 12 ⋅ x − 2 ⋅ x 2 + 4 ⋅ x = 16 ⋅ x − 2 ⋅ x 2
MCB = M[1] + M[2 ]CB = 12 ⋅ x − 2 ⋅ x 2 + 12 − 2 ⋅ x = 12 + 10 ⋅ x − 2 ⋅ x 2
Para determinar el máximo momento flector, derivamos ambas
expresiones e igualamos a cero:
M' AC = 16 − 4 ⋅ x = 0 → x = 4
M'CB = 10 − 4 ⋅ x = 0 → x = 2.5
El primer valor obtenido no tiene significado físico, pues el punto de
abcisa x=4 no pertenece al intervalo AC. Por consiguiente, el máximo momento
flector se da en la sección de la viga distante 2.5 m del apoyo dorsal.
El valor de este momento máximo es:
M x =2.5 = 12 + 10 ⋅ 2.5 − 2 ⋅ 2.5 2 = 24.5 m ⋅ T
7Obtención del esfuerzo cortante máximo
Operamos de igual modo:
3
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Q AC = Q [1] + Q [2 ]AC = 12 − 4 ⋅ x + 4 = 16 − 4 ⋅ x
Q CB = Q [1] + Q [2 ]CB = 12 − 4 ⋅ x − 2 = 10 − 4 ⋅ x
Se puede comprobar que ambas expresiones son dos rectas. Para
estudiar donde se encuentra el esfuerzo cortante máximo, analizaremos las
secciones donde existen cargas concentradas (apoyos y punto C).
A
B
C
Q A = Q x =0 = 16 − 4 ⋅ 0 = 16T
Q B = Q x =6 = 10 − 4 ⋅ 6 = −14T
Q C = Q ACx =2 + Q CBx =2 = (16 − 4 ⋅ 2) − (10 − 4 ⋅ 2) = 6T
Por tanto, el esfuerzo cortante máximo se da en el apoyo A.
7Obtención de la flecha
Para obtener la deformación máxima es preciso estudiar previamente la
deformada, que habrá que analizarla por tramos:
y AC = y [1] + y [2 ]AC =
(
)
(
x
4⋅x
⋅ x 3 − 12 ⋅ x 2 + 216 +
⋅ 20 − x 2
6 ⋅E ⋅I
6 ⋅E ⋅I
)
4
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
y AC =
[ (
)
)]
(
(
1
1
⋅ x ⋅ x 3 − 12 ⋅ x 2 + 216 + 4 ⋅ x ⋅ 20 − x 2 =
⋅ x 4 − 16 ⋅ x 3 + 296 ⋅ x
6 ⋅E ⋅I
6 ⋅E ⋅I
y CB = y [1] + y [2 ]CB =
[ (
(6 − x ) ⋅ − 4 + 12 ⋅ x − x 2
x
⋅ x 3 − 12 ⋅ x 2 + 216 +
3 ⋅E ⋅I
6 ⋅E ⋅I
(
)
(
)
y CB =
1
⋅ x ⋅ x 3 − 12 ⋅ x 2 + 216 + (12 − 2 ⋅ x ) ⋅ ( −4 + 12 ⋅ x − x 2 )
6 ⋅E ⋅I
y CB =
1
⋅ x 4 − 10 ⋅ x 3 − 36 ⋅ x 2 + 368 ⋅ x − 48
6 ⋅E ⋅I
[
)
]
]
Una vez obtenida la deformada, estudiamos la flecha:
y' AC = 0 →
(
)
1
⋅ 4 ⋅ x 3 − 48 ⋅ x 2 + 296 = 0
6 ⋅E ⋅I
Las raíces de este polinomio son: x=-2.28, x=2.84 y x=11.43. Todos
estos valores no tienen significado físico, pues no pertenecen al intervalo AC.
y' CB = 0 →
(
)
1
⋅ 4 ⋅ x 3 − 30 ⋅ x 2 − 72 ⋅ x + 368 = 0
6 ⋅E ⋅I
Las raíces de este polinomio son: x=2.93, x=-3.77 y x=8.34. Por tanto, la
deformación máxima se produce en la sección distante del apoyo A 2.93 m.
y x =2.93 =
1
90.56
⋅ (2.93 4 − 10 ⋅ 2.93 3 − 36 ⋅ 2.93 2 + 368 ⋅ 2.93 − 48) =
6 ⋅E ⋅I
E ⋅I
teniendo en cuenta que las unidades son T y m.
5
)