Ejemplos 5.1 a) Determinar por tabla los valores percentiles indicados
Anuncio

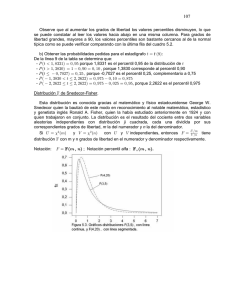
104 Ejemplos 5.1 a) Determinar por tabla los valores percentiles indicados: - ;#!ß!& Ð"&Ñ œ (ß #'" ; ;#0,90 Ð15Ñ œ ##ß $!( los que se encuentran en la línea 15 columnas 0,05 y 0,90 respectivamente - ;#!ß!& Ð*Ñ œ $ß $#& ; ;#!ß*! Ð*Ñ œ "%ß ')% se buscan en las mismas columnas en línea 9. Observe que al aumentar los grados de libertad los valores percentiles son mayores concordante con la observación 1 anterior. # Ð"#Ñ œ #"ß !#' los valores percentiles de la ji cuadrado son - ;#!ß!& Ð"#Ñ œ &ß ##' à ;!ß*& siempre positivos (ver figura 5.1) a diferencia de lo que ocurre en la normal estándar. b) Obtener las probabilidades pedidas para el estadígrafo H# œ ;# Ð#!Ñ Þ De la línea 20 de la tabla se determina que: - T ÐH# "!ß )&Ñ œ !ß !& porque 10,85 es el percentil 0,05 de la distribución de ;# Ð#!Ñ . - T ÐH# #)ß %"Ñ œ " !ß *! œ !ß "! ß porque 28,41 corresponde al percentil 0,90. - T (*ß &* Ÿ H# Ÿ $%ß "(Ñ œ !ß *(& !ß !#& œ !ß *& ß porque 34,17 y 9,59 son los percentiles 0,975 y 0,025 respectivamente. En el siguiente teorema se enunciarán, sin demostración, las propiedades reproductivas de la distribución ji cuadrada que son de interés.






![[Word2000]](http://s2.studylib.es/store/data/003178609_1-2cd79220e7dda4da73122b9835f65b9f-300x300.png)


