PERCENTILES_Y_CUARTILES_DE_UNA_DISTRIBUCI_N

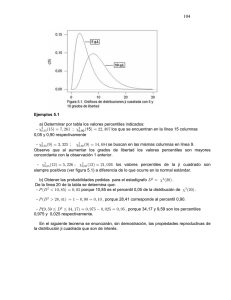
PERCENTILES Y CUARTILES DE UNA DISTRIBUCIÓN
Un percentil da información acerca de cómo se distribuyen los datos sobre un intervalo, desde el
menor hasta el mayor. El pésimo percentil es un valor tal que por lo menos p% de las
observaciones son menores o iguales que este valor y por lo menos (100 – p) % de las
observaciones son mayores o iguales que este valor. De acuerdo a esta definición se pueden
calcular 99 percentiles, es decir, P1, P2, P3,…., P99 que dividen la muestra ordenada en 99 partes
que contienen aproximadamente el mismo numero de datos, es decir que el 1% de los datos son
menores que P1, el 5% de los datos son menores que P5, el 40% de los datos son menores que P40
y el 99% de los datos son menores que P99.
Una de las medidas cada vez mas utilizadas, son los cuartiles, que son tres valores Q1, Q2, Q3 que
dividen la muestra ordenada en cuatro partes que contienen aproximadamente el mismo numero
de datos, es decir que el 25% de los datos son menores que Q1, el 50% de los datos son menores
que Q2 y el 75% de los datos son menores que Q3. Estos tres valores producen una muy buena
síntesis de la distribución de frecuencias.
Nótese que siempre entre los valores Q1 y Q3, se encuentra el 50% central de los datos.
Ejemplo 1
La siguiente tabla de frecuencias contiene información acerca del número de personas que
conforman los hogares de un barrio del sur de Cali: Calculemos algunos percentiles, por ejemplo:
Note que el 10% (H1) de los datos son menores o iguales a 3, es decir, P10 = 3.
El 10% de los hogares están conformados máximos por 3 personas. Esto significa que el 90%
restante está conformado mínimo por 3 personas.
Note que el 24% (H2) de los datos son menores o iguales a 4, es decir, P24 = 4. El 24% de los
hogares están conformado máximo por 4 personas.
Ahora, puede observar que P50 = 5, el 50% de los hogares están conformados máximo por 5
personas. Entonces P50 = Me.
P85 = 6, el 85% de los hogares están conformados máximo por 6 personas.
3 5 0,10 10%
4 7 0,14 24%
5 20 0,40 64%
6 13 0,26 90%
7 4 0,08 98%
8 1 0,02 100%Calculemos los cuartiles para el ejemplo anterior.
Note que el 24% (H2) de los datos son menores o iguales a 4, el 64% (H3) de los datos son
menores o iguales a 5, es decir, 5 es el Q1. Esto quiere decir que: H (Q1)=25%. También se puede
observar que 5 es el Q2. Es claro que Q2 = Me. Observe que el 90% (H4) de los datos son menores
o iguales a 6, significa que 6 es el Q3.
Ejemplo 2
La siguiente tabla de frecuencias representa los datos de una variable continua.
Intervalo Frecuencia Frecuencia Frecuencia acumulada de clase absoluta ni relativa hi absoluta
(Ni) relativa (Hi )
(10,20] 6 0.12 6 0.12
(20,30] 8 0.16 14 0.28
(30,40] 21 0.42 35 0.70
(40,50] 13 0.26 48 0.96
(50,60] 2 0.04 50 1.00
50 1.00
Calculemos algunos percentiles y cuartiles, por ejemplo:
Se desea encontrar el Segundo cuartil Q2, tal que el 50% de los datos son menores o iguales a este
valor, es decir: H (Q2) = 50%. Al observar la tabla de frecuencias encontramos que H (30) = 28% y H
(40) = 70%, lo cual nos indica que el segundo cuartil Q2, se encuentra entre 30 y 40.
Siguiendo el proceso anterior, para H (Q3) = 75%, se obtiene que H (40) = 70% y H (50) = 96%, lo
cual nos indica que el tercer cuartil Q3, se encuentra entre 40 y 50.
Para el percentil 15, tenemos que H (P15) = 15%, se obtiene que H (20) = 12% y H (30) = 28%, lo
cual nos indica que el P15, se encuentra entre 20 y 30.
Para el percentil 86, tenemos que H (P86) = 86%, se obtiene que H (40) = 70% y H (50) = 96%, lo
cual nos indica que el P86, se encuentra entre 40 y 50.
A la distancia entre los cuartiles Q1 y Q3, se le llama rango intercuartílico. Rango intercuartílico
(RIC) = Q3 - Q1.