Principio de Trabajo-Energía en 2 y 3 dimensiones
Anuncio
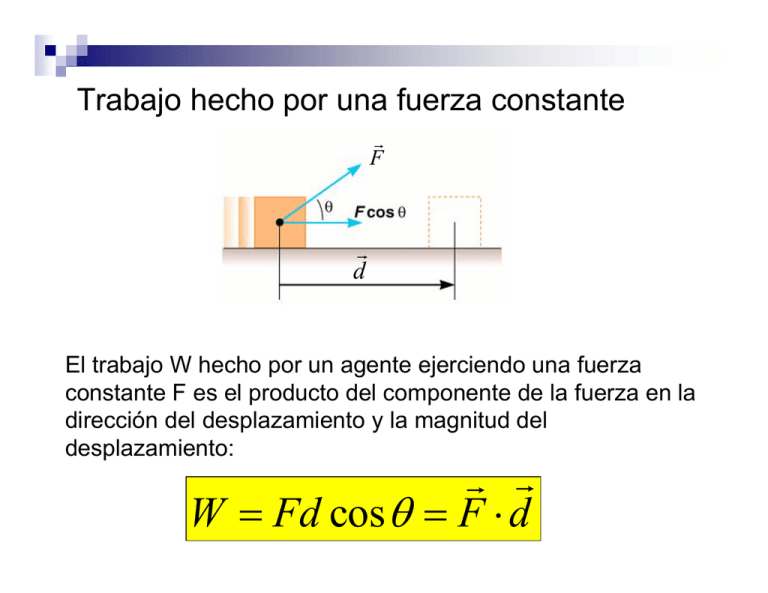
Trabajo hecho por una fuerza constante G F G d El trabajo W hecho por un agente ejerciendo una fuerza constante F es el producto del componente de la fuerza en la dirección del desplazamiento y la magnitud del desplazamiento: G G W = Fd cos θ = F ⋅ d Trabajo hecho por una fuerza constante NOTA: El trabajo es cero si el bloque no se mueve. También es cero si hay movimiento, pero la fuerza no tiene componente en la dirección del desplazamiento. G F G d Si la fuerza es en Newtons y el desplazamiento en metros, entonces el trabajo es en Julios: 1 J =1 N ⋅m Trabajo hecho por una fuerza variable G F Fx dx dW = Fx dx xf W = ∫ Fx dx xi El trabajo es igual al área bajo la curva de fuerza paralela versus desplazamiento. Principio de Trabajo-Energía G F Fx dx W =∫ xf xi Fx dx dv Fx = max = m dt dv dv dx dv = =v dt dx dt dx dv Fx dx = m dx = mvdv dt Principio de Trabajo-Energía Cinética xf vf xi vi Wneto = ∫ Fx dx = ∫ mvdv Wneto 1 2 1 2 = mv f − mvi 2 2 La cantidad 1/2mv2 se conoce como la energía cinética K. La ecuación anterior dice que el trabajo neto o total es igual al cambio en la energía cinética. Wneto = ∆K Potencia P ~ razón a la cual se hace trabajo G G dW P= dW = F ⋅ ds , dt G G ds G G P=F⋅ = F ⋅v dt La unidad de potencia es el vatio (W ). J 1W = 1 s Ejemplo Un pequeño motor mueve un ascensor que eleva una carga de ladrillos de peso 800 N a una altura de 10 m en 20 s. ¿Cuál es la potencia mínima que debe suplir el motor?. La fuerza F más pequeña que puede ejercer el motor (esta fuerza es la tensión en la cuerda) es de 800 N. En ese caso el bloque se mueve hacia arriba sin aceleración (velocidad constante ). Trabajo hecho por la fuerza de gravedad Partícula subiendo: W = mgd cos180 = − mgd D W = ∆K = − mgd El signo negativo significa que la energía cinética se reduce. Partícula bajando: W = mgd cos 0 = + mgd W = ∆K = + mgd D El signo positivo significa que la energía cinética aumenta. Ejemplo: Una caja de 15 kg, inicialmente en reposo, se mueve cuesta arriba mediante un cable. La caja se desplaza una distancia d = 5.7 m hasta llegar a una altura h = 2.5 m donde se detiene. Calcula (a) el trabajo hecho por la fuerza de gravedad y (b) el trabajo hecho por la tensión en el cable. Trabajo hecho por un resorte Ley de Hooke G G F = −kd Para movimiento en x: F = −kx xf xf xi xi Wr = ∫ Fdx = ∫ ( −kx ) dx ⎛ 1 ⎞ 2 xf ⎛ 1 ⎞ 2 Wr = ⎜ − k ⎟ x = ⎜ − k ⎟ ( x f − xi2 ) ⎝ 2 ⎠ xi ⎝ 2 ⎠ ⎛1 2 1 2⎞ Wr = − ⎜ kx f − kxi ⎟ Ver ejemplo 2 ⎝2 ⎠ 7-7.










