Solucions a “Ejercicis i problemes”
Anuncio
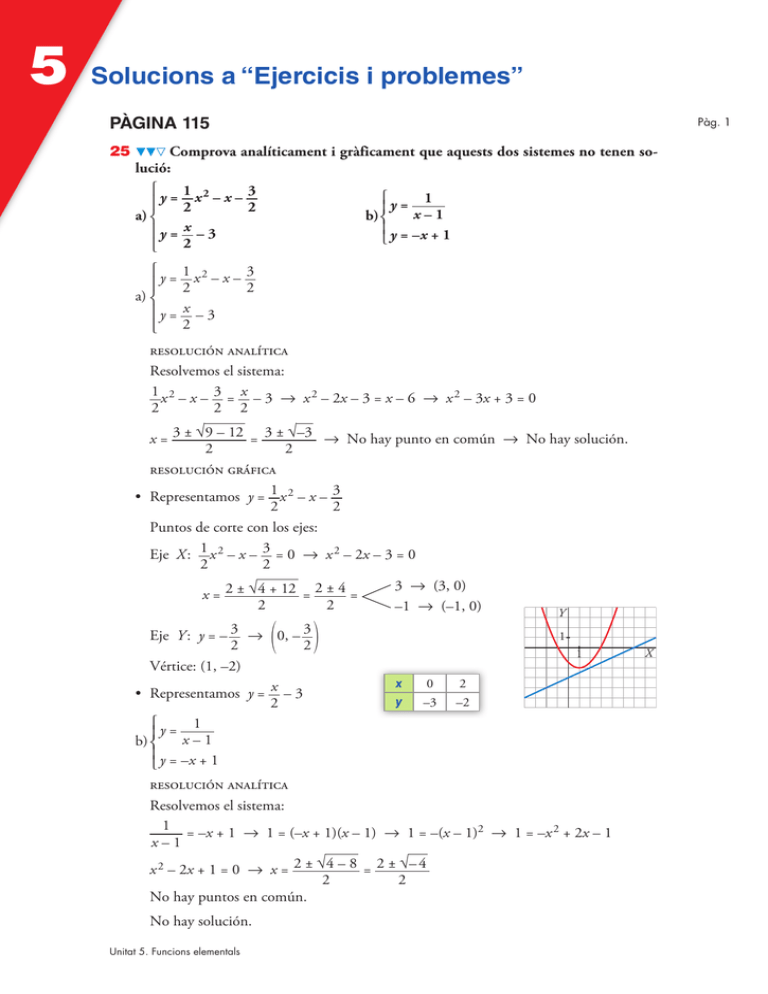
5 Solucions a “Ejercicis i problemes” PÀGINA 115 25 Pàg. 1 Comprova analíticament i gràficament que aquests dos sistemes no tenen solució: °y = § a)¢ §y = £ 1 x 2 – x – 3 2 2 x –3 2 °y = § a)¢ §y = £ 1 x 2 – x – 3 2 2 x –3 2 °y = 1 b)§¢ x – 1 § y = –x + 1 £ resolución analítica Resolvemos el sistema: 1 x 2 – x – 3 = x – 3 8 x 2 – 2x – 3 = x – 6 8 x 2 – 3x + 3 = 0 2 2 2 x = 3 ± √9 – 12 = 3 ± √–3 8 No hay punto en común 8 No hay solución. 2 2 resolución gráfica • Representamos y = 1 x 2 – x – 3 2 2 Puntos de corte con los ejes: Eje X : 1 x 2 – x – 3 = 0 8 x 2 – 2x – 3 = 0 2 2 x = 2 ± √4 + 12 = 2 ± 4 = 2 2 ( ) 3 8 (3, 0) –1 8 (–1, 0) Y 1 Eje Y : y = – 3 8 0, – 3 2 2 1 Vértice: (1, –2) x 0 2 • Representamos y = x – 3 y –3 –2 2 °y = 1 b)§¢ x – 1 § y = –x + 1 £ resolución analítica Resolvemos el sistema: 1 = –x + 1 8 1 = (–x + 1)(x – 1) 8 1 = –(x – 1)2 8 1 = –x 2 + 2x – 1 x–1 x 2 – 2x + 1 = 0 8 x = 2 ± √4 – 8 = 2 ± √– 4 2 2 No hay puntos en común. No hay solución. Unitat 5. Funcions elementals X 5 Solucions a “Ejercicis i problemes” resolución gráfica •Representamos y = x y 0 –1 –1 –1/2 Pàg. 2 1 x–1 2 1 Y 3 1/2 2 2 •Representamos y = –x + 1 x 26 y 0 1 X 2 –1 Resol analíticament i gràficament els sistemes següents: °y = 2 ° y = √x + 1 a)§¢ x + 2 b)¢ § y = 3x + 2 £y = x – 5 £ °y = 2 a)§¢ x + 2 § y = 3x + 2 £ resolución analítica Resolvemos el sistema: 2 = 3x + 2 8 3x 2 + 8x + 2 = 0 x+2 x1 ≈ –0,28 8 y1 ≈ 1,16 x = –8 ± √64 – 24 = –8 ± √40 6 6 x2 ≈ –2,39 8 y2 ≈ –5,17 resolución gráfica •Representamos la función y = x y 4 –1 –1 2 0 1 2 que tiene una asíntota en x = –2 y otra en y = 0: x+2 1 2/3 •Representamos la recta y = 3x + 2 x y –2 – 4 0 2 ° y = √x + 1 b)¢ £y = x – 5 resolución analítica Puntos de corte: √x + 1 = x – 5 8 x + 1 = (x – 5)2 8 x + 1 = x 2 – 10x + 25 x 2 – 11x + 24 = 0 8 x = 11 ± √121 – 96 = 2 x = 8 8 y = 3 = 11 ± 5 2 x = 3 8 y = –2 8 no pertenece a y = √x + 1. Solución: (8, 3) Unitat 5. Funcions elementals Y 2 2 X 5 Solucions a “Ejercicis i problemes” resolución gráfica Pàg. 3 •Para representar y = √x + 1 damos valores: x y –1 0 3 2 0 1 8 3 Y •Para representar y = x – 5, hacemos la tabla de valores: x 27 y 3 –2 8 3 (8, 3) X 3 –2 a) Calcula b i c perquè el vèrtex de la paràbola y = x 2 + bx + c estiga en el punt (3, 1). b)Quin n’és l’eix de simetria? c)Quins són els punts de tall amb els eixos? a)Vértice en x = 3 8 – b = 3 8 –b = 6a = 6 8 b = –6 2a Pasa por (3, 1) 8 1 = 9 – 18 + c 8 c = 10 y = x 2 – 6x + 10 b)Su eje de simetría es x = 3. c)Cortes con los ejes: x = 0 8 y = 10 8 Punto (0, 10) x 2 – 6x + 10 = 0 8 x = 6 ± √36 – 40 8 No tiene solución, por tanto, no corta al 2 eje X. 28 La paràbola y = ax 2 + bx + c passa per l’origen de coordenades. Quant valdrà c? Si, a més, saps que passa pels punts (1, 3) i (4, 6), troba a i b i representa’n la paràbola. c = 0 y= ax 2 Y 6 + bx (1, 3) 8 3 = a + b ° a = 3 – b 8 a = –1/2 ¢ (4, 6) 8 6 = 16a + 4b £ 6 = 16(3 – b) + 4b 8 b = 7/2 y = – 1 x 2 + 7 x 2 2 29 Calcula a i b perquè la funció y = a 2–b –1 = a –1 – b 2= 1 4 a passe pels punts (2, 2) i (–1, –1). x–b ° § a = 4 – 2b ° 1 + b = 4 – 2b 8 b = 1 ° 2 ¢ ¢ y=x–1 ¢ £ § a=1+b £ a=2 £ Unitat 5. Funcions elementals 3 X Solucions a “Ejercicis i problemes” 30 El gràfic d’una funció exponencial del tipus y = ka x passa pels punts (0, 3) i (1; 3,6). a)Calcula k i a. b) És creixent o decreixent? c) Representa la funció. a)Si pasa por el punto (0, 3) 8 3 = ka 0 8 k = 3 Si pasa por el punto (1; 3,6) 8 3,6 = ka 1 8 3,6 = 3a 8 a = 1,2 Y Tenemos la función y = 3 · (1,2) x b)Es una función creciente. c)Hacemos una tabla de valores: 6 x y –2 –1 2,08 2,5 0 3 3 1 2 3 3,6 4,32 5,18 –3 –1 31 1 3 X La funció exponencial y = ka x passa pels punts (0, 2) i (2; 1,28). Calcula k i a i representa la funció. y = ka x Pasa por el punto (0, 2): 2 = k · a 0 8 2 = k Pasa por (2; 1,28): 1,28 = k · a 2 8 1,28 = 2a 2 8 a 2 = 0,64 8 a = 0,8 Y La función es: y = 2 · (0,8) x x y –3 –2 –1 3,906 3,125 2,5 0 2 1 2 3 1,6 1,28 1,024 1 1 32 X a) Representa gràficament la funció exponencial y = 1,2x fent ús d’una taula de valors. b)Quina és la funció inversa o recíproca de y = 1,2x ? Representa-la en els mateixos eixos. La función inversa de y = 1,2x es y = log 1,2 x. 16 y – 4 0 1 2 4 8 10 12 16 0,48 1 1,2 1,44 2,07 4,3 6,2 8,9 18,5 Unitat 5. Funcions elementals 14 12 y = log1,2 x 10 x x y= 5 8 6 y = 1,2x 4 2 –4 2 –4 4 6 8 10 12 14 16 Pàg. 4 5 Solucions a “Ejercicis i problemes” 33 Representa les funcions següents: °x 2 b)f (x) = §¢ 1 §x £ b) Y si x < 0 °x a)f (x) = ¢ £√x si x Ó 0 a) Pàg. 5 Y si x < 1 si x Ó 1 X 34 X a) Representa la funció y = | x |, on | x | és el valor absolut de x. °–x si x < 0 b)Representa: y = ¢ £x si x Ó 0 Compara els dos gràfics, a) i b). Y a) y b) son la misma gráfica. X 35 Fes el gràfic de les funcions següents: a)y = | x – 1| b)y = 1 + | x | a) b) Y Y X X ■Resol problemes 36 Quina és l’equació de la funció que ens dóna el perímetre d’un quadrat depenent de quant en mesure el costat? I la que ens en dóna l’àrea? Dibuixa ambdues funcions. Si l es el lado del cuadrado, Y P = 4l A=l 2 P = 4l A = l2 X Unitat 5. Funcions elementals 5 Solucions a “Ejercicis i problemes” 37 Una casa de reprografia cobra 5 cent. per cada fotocòpia. Oferix també un servei de multicòpia, pel qual cobra 50 cent. fixos i 2 cent. per cada còpia d’un mateix exemplar. Fes, per a cada cas, una taula de valors que mostre el que cal pagar segons el nombre de còpies realitzades. Representa les funcions obtingudes. Té sentit unir els punts en cada una d’aquestes? Obtín l’expressió analítica de cada funció. A partir de quantes còpies és més econòmic utilitzar la multicopista? fotocòpies multicòpia unitats preu unitats preu 1 5 1 52 5 25 5 60 10 50 10 70 14 70 14 78 18 90 18 86 20 100 20 90 PRECIO 100 50 10 2 10 15 20 NÚMERO DE COPIAS No tiene sentido unir los puntos; solo se pueden dar valores naturales. Expresiones analíticas: Fotocopias: y = 5x Multicopias: y = 50 + 2x A partir de 17 copias, es más económico utilizar la multicopista. Unitat 5. Funcions elementals Pàg. 6