4.5 Distribución de Bernoulli. Existen experimentos
Anuncio
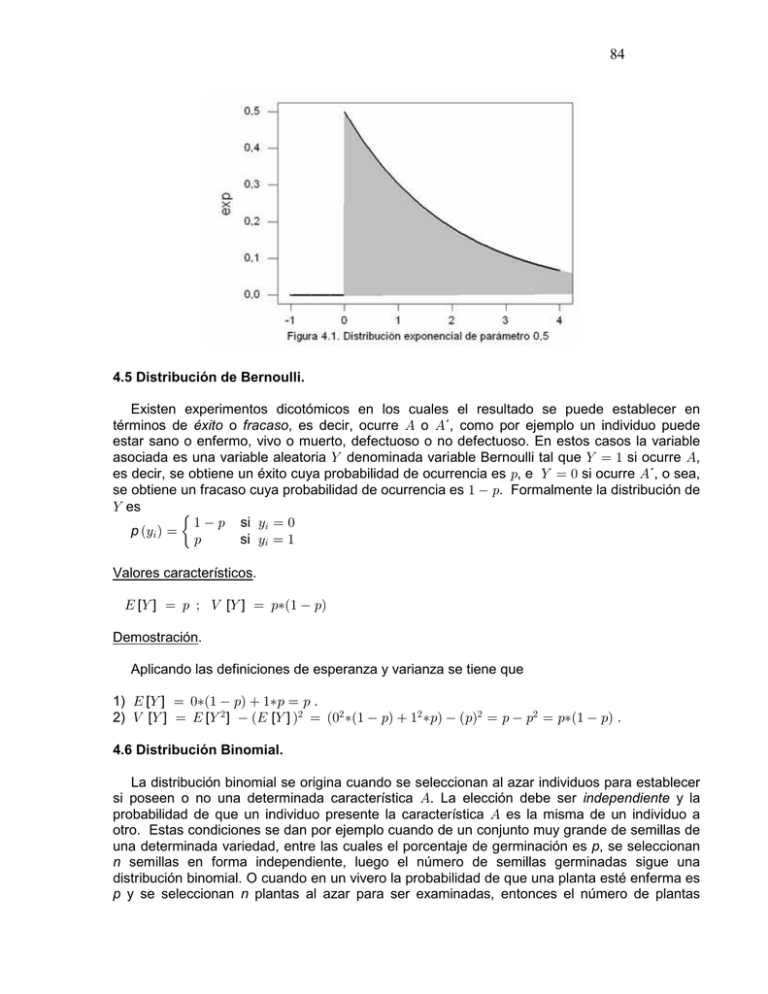
84 4.5 Distribución de Bernoulli. Existen experimentos dicotómicos en los cuales el resultado se puede establecer en términos de éxito o fracaso, es decir, ocurre E o E´, como por ejemplo un individuo puede estar sano o enfermo, vivo o muerto, defectuoso o no defectuoso. En estos casos la variable asociada es una variable aleatoria ] denominada variable Bernoulli tal que ] œ " si ocurre E, es decir, se obtiene un éxito cuya probabilidad de ocurrencia es :, e ] œ ! si ocurre E´, o sea, se obtiene un fracaso cuya probabilidad de ocurrencia es " :. Formalmente la distribución de ] es " : si C3 œ ! p ÐC3 Ñ œ œ : si C3 œ " Valores característicos. I [] ] œ : à Z [] ] œ :‡Ð" :Ñ Demostración. Aplicando las definiciones de esperanza y varianza se tiene que 1) I [] ] œ !‡Ð" :Ñ "‡: œ : . 2) Z [] ] œ I [] # ] ÐI [] ] Ñ# œ Ð!# ‡Ð" :Ñ "# ‡:Ñ Ð:Ñ# œ : :# œ :‡Ð" :Ñ . 4.6 Distribución Binomial. La distribución binomial se origina cuando se seleccionan al azar individuos para establecer si poseen o no una determinada característica E. La elección debe ser independiente y la probabilidad de que un individuo presente la característica E es la misma de un individuo a otro. Estas condiciones se dan por ejemplo cuando de un conjunto muy grande de semillas de una determinada variedad, entre las cuales el porcentaje de germinación es p, se seleccionan n semillas en forma independiente, luego el número de semillas germinadas sigue una distribución binomial. O cuando en un vivero la probabilidad de que una planta esté enferma es p y se seleccionan n plantas al azar para ser examinadas, entonces el número de plantas











