EN UNA FAMILIA DE 7 HIJOS, ¿CUÁL ES LA PROBABILIDAD DE

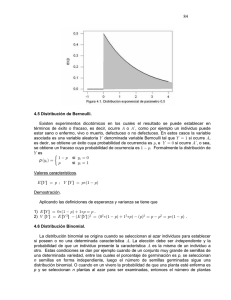
EN UNA FAMILIA DE 7 HIJOS, ¿CUÁL ES LA PROBABILIDAD DE QUE AL
MENOS CINCO HIJOS SEAN NIÑOS?
Para poder resolver este problema primero hay que tener algunos conocimientos sobre
probabilidad:
- Una distribución binomial es una distribución de probabilidad que sirve para contar el
número de éxitos que buscas en una secuencia de n ensayos, donde la probabilidad de
éxitos, que siempre es fija, se denomina p. Esta función de probabilidad se utiliza para
calcular probabilidades en las que solo hay dos posibles resultados (éxito o fracaso). La
probabilidad de fracaso se denomina por q y es q=1-p.
-
Para representar que una variable aleatoria X sigue una distribución binomial de
parámetros n y p, se escribe:
La fórmula de la binomial es:
El problema dice que en una familia de 7 hijos (por tanto n=7) al menos 5 sean niños. Al decir
“al menos” hay que tener en cuenta que pueden ser 5, 6 o 7 hijos niños, por ello hay que
calcular la probabilidad de X=5+X=6+X=7, siendo X el número posible de niños.
Teniendo en cuenta que la probabilidad de que al tener un hijo este sea niño, es la misma que
la probabilidad de que sea niña, tomamos como número de éxitos p= ½, por tanto como
q=1-p, entonces q= ½.
Para resolver el problema utilizamos la fórmula de la Binomial siendo X Bin (7, ½)
P(X=5) =
0,1640626
P(X=6) =
0,0546875
P(X=7) =
0,0078125
Hay que tener en cuenta que como dice “al menos cinco” también hay que contar con que
haya más de 5 niños, ya que se seguiría cumpliendo la pregunta, por ello se suman todas las
probabilidades, P(X=5) + P(X=6) + P(X=7) dando como resultado 0,2265625, que es la
probabilidad de que en una familia de 7 hijos al menos 5 sean niños.
P(7 hijos donde al menos 5 sean niños)= 0,1640626+0,0546875+0,0078125=0,2265625
Leire Echepare Olivera