Los tipos más habituales de variables aleatorias
Anuncio

Universidad Autónoma de Madrid
2o de Biologı́a. Estadı́stica.
Los tipos más habituales de variables aleatorias
Nota. En todos los casos denotamos por Ω el espacio muestral, es decir el conjunto de los posibles
valores que puede tomar la variable.
Bernoulli. Es una variable con Ω = {0, 1} (dos elementos). Decimos que X es una Bernoulli (p) si
P (X = 1) = p, en cuyo caso es P (X = 0) = 1 − p.
si X ∼ Bernoulli(p) , entonces X tiene
E(X) = p
V (X) = p (1 − p)
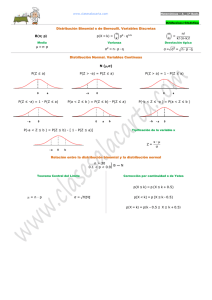
Binomial. La variable X es una binomial B(n, p) si es X = X1 +X2 +· · ·+Xn siendo las X1 , . . . , Xn
(conjuntamente) independientes y todas ellas Bernoulli (p).
Tiene Ω = {0, 1, 2, . . . , n} (n + 1 elementos). Aunque la varianza de una suma no siempre es la
suma de las varianzas, sı́ lo es para sumandos independientes. Por lo tanto:
E(X) = n p
si X ∼ B(n, p) , entonces X tiene
V (X) = n p (1 − p)
Para una binomial, la probabilidad de un intervalo [a, b] con 0 ≤ a < b ≤ n es:
X n
P (a ≤ X ≤ b) =
pj (1 − p)n−j .
j
j entero
a≤j≤b
Poisson. La variable X es una Poisson(λ) si es un lı́mite de variables B(n, p) con n → ∞ y np → λ.
Aquı́ λ es un número real positivo.
Tiene Ω = {0, 1, 2, 3, . . . } (todos los enteros no negativos), luego es discreta. La probabilidad de
un intervalo [a, b] con 0 ≤ a < b es:
X
P (a ≤ X ≤ b) =
j
entero
e−λ
λj
.
j!
a≤j≤b
Tomando n→∞
lim en las fórmulas de valor esperado y varianza de la binomial, sacamos:
np→λ
E(X) = λ
V (X) = √λ
si X ∼ Poisson(λ) , entonces X tiene
σX
=
λ
Normal. La variable X es una normal N (µ, σ) si es una variable continua, con Ω = R, y su densidad
de probabilidad es:
(x − µ)2
−
1
2 σ2 .
f (x) = √
·e
2π σ
Se comprueba que esta f (x) cumple lo siguiente:
R∞
R∞
R∞
2
2
f
(x)
dx
=
1,
x
f
(x)
dx
=
µ
y
−∞
−∞
−∞ (x − µ) f (x) dx = σ ,
luego efectivamente f (x) es una densidad de probabilidad, y además:
E(X) = µ
V (X) = σ 2
si X ∼ N (µ, σ) , entonces X tiene
σX
= σ
1
Exponencial. La variable X es una Exponencial (λ) si es una variable continua, con Ω = R, y su
densidad de probabilidad es:
λ e−λx si x ≥ 0
f (x) =
0
si x < 0
Propiedades de las normales
Sean a, c constantes reales, la c positiva. Entonces:
X + a ∼ N( µ + a , σ )
si X ∼ N (µ, σ), entonces
cX
∼ N ( cµ , cσ )
De ahı́ resulta:
si X ∼ N (µ, σ) , entonces
X −µ
= Z ∼ N (0, 1)
σ
o sea, que al tipificar un normal X resulta una variable Z que es normal estándar.
Si X ∼ N (µ, σ),
Si X ∼ N (µ1 , σ1 ),
entonces
−X ∼ N (−µ, σ).
Y ∼ N (µ2 , σ2 )
X +Y
X −Y
y X, Y son independientes, entonces:
q
2
2
∼ N µ1 + µ2 , σ1 + σ2
q
2
2
∼ N µ1 − µ2 , σ1 + σ2 .
Más en general, si Xj ∼ N (µj , σj ) para 1 ≤ j ≤ k
y X1 , . . . , Xk son (conjuntamente)
independientes, entonces:
q
2
2
.
X1 + · · · + Xk ∼ N µ1 + · · · + µk , σ1 + · · · + σk
Aproximaciones de la binomial
1. Cuando n es grande pero np no es grande, aproximamos una variable X ∼ B(n, p) por una
variable Y ∼ Poisson (λ) que cumpla E(Y ) = E(X), es decir λ = np:
B(n, p) ∼ X ≈ Y ∼ Poisson (np) .
2. Cuando n es grande y np se sale de los valores de λ en las tablas de la Poisson, aproximamos
una variable binomial X ∼ B(n, p) por una variable normal Y ∼ N (µ, σ) que cumpla
E(Y ) = E(X)
es decir
y
V (Y ) = V (X) ,
µ = n p y σ 2 = n p (1 − p). Puesto de otra manera:
p
B(n, p) ∼ X ≈ Y ∼ N n p , n p (1 − p) .
2







![[ ] [ ] np [ ] npq [ ] [ ] λ [ ] λ [ ] µ [ ] 2](http://s2.studylib.es/store/data/007002888_1-705516d827e27927517f29d628d99e04-300x300.png)