Introducción
Anuncio

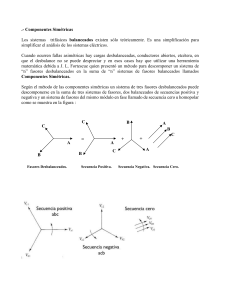
1. Introducción Un sistema polifásico desequilibrado se puede estudiar directamente aplicando las leyes de Kirchhoff a la red. No obstante este procedimiento de cálculo directo es laborioso, al tener que trabajar con un gran número de ecuaciones. Las tensiones, intensidades o impedancias están representadas por magnitudes vectoriales complejas, por lo que el número de ecuaciones se duplica, complicando aún más su resolución. El procedimiento más cómodo para estudiar regímenes desequilibrados polifásicos es el llamado método de las componentes simétricas, y más raramente método de las coordenadas simétricas. El procedimiento se basa en la propiedad de las magnitudes sinusoidales de que: q vectores cualesquiera pueden considerarse como la suma de q sistemas de q vectores. El método más empleado y conocido para descomponer un sistema de n vectores en n sistemas simétricos, es el de las componentes simétricas, conocido también por método de Fortescue, que lo propuso en 1918 en su trabajo “Method of Simetrical Coordinates Applied to the Solution of Polyfase Networks” y que fué estudiado simultáneamente por Fortescue y por Stokvis. El método consiste básicamente en descomponer un sistema polifásico asimétrico en varios simétricos, que podemos estudiar fácilmente mediante un circuito monofásico equivalente. Posteriormente aplicamos el principio de superposición para obtener la respuesta del circuito original, quedando simplificados así notablemente el trabajo de resolución del circuito original. Vamos a estudiar solamente el caso de sistemas de tres fases, que es el de nuestro interés, pudiendo generalizarse el método a circuitos de q fases. Es preciso observar que la descomposición de las tensiones y corrientes reales de un circuito, en sus componentes simétricas, es un procedimiento de trabajo para calcular su valor en sistemas desequilibrados. No obstante, estos valores simétricos no son solamente un artificio de cálculo, sino que en cierto modo tienen una realidad física que permiten su medida. Ciertamente, las componentes simétricas no aparecen aisladas en un circuito y podemos comprobar que su presencia produce una serie de fenómenos físicos observables que serán diferentes según la componente considerada. Por ejemplo, en un circuito trifásico desequilibrado con conductor neutro, la corriente de neutro es tres veces la componente homopolar de las corrientes reales en fase. En un motor trifásico alimentado por un sistema de tensiones desequilibradas, la componente directa engendra un campo giratorio en el sentido de giro del rotor, produciendo un par útil; la componente inversa produce un campo en sentido inverso, creando un par de frenado, y la componente homopolar no produce ningún efecto. La aplicación del método de componentes simétricas se emplea principalmente para el estudio de circuitos desequilibrados, como la determinación de corrientes en circuitos con receptores distintos sobre las tres fases, ejemplo: soldaduras, hornos, tracción, etc. Se emplea para el estudio de las corrientes de cortocircuito, que es un caso particular de desequilibrio. Se emplea igualmente para el diseño de aparatos de protección que son indiferentes a la carga de la red y funcionan en el caso de averías disimétricas (cortocircuitos), así como para el estudio de problemas relacionados con máquinas rotatorias.