Tema 2
Anuncio

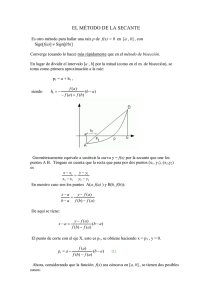
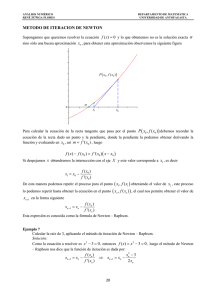
SOLUCIÓN NUMÉRICA DE ECUACIONES ALGEBRAICAS Y TRASCENDENTES • EL PROBLEMA DE OBTENER LOS CEROS O RAÍCES DE UNA ECUACIÓN ALGEBRAICA O TRASCENDENTE, ES UNO DE LOS REQUERIDOS MAS FRECUENTEMENTE, DEBIDO A ELLO EL NÚMERO DE MÉTODOS PARA RESOLVER ESTE PROBLEMA ES EXTENSO Y VARIADO, LOS HAY PARA PARA RAÍCES REALES, COMPLEJAS, COMBINADOS, PARA CONOCER UNA O TODAS LAS RAÍCES. ACTUALMENTE, DADO EL DESARROLLO DE LAS COMPUTADORAS, ÁQUELLOS MÉTODOS QUE SEAN MAS EFICIENTES Y SUSCEPTIBLES DE AUTOMATIZARSE SON LOS QUE PARA EL ANÁLISIS NUMÉRICO PRESENTAN MAYOR UTILIDAD, TAL ES EL CASO DE LOS MÉTODOS ITERATIVOS O MÉTODOS DE APROXIMACIONES SUCESIVAS. TRATANDOSE DE ECUACIONES ALGEBRAICAS SE TIENEN MÉTODOS EXACTOS PARA RESOLVER LAS ECUACIONES DE SEGUNDO Y TERCER GRADO, PARA LOS DE CUARTO GRADO EXISTE EL MÉTODO DE BROWN Y PARA GRADOS SUPERIORES NO EXISTEN MÉTODOS DE LOS LLAMADOS “EXACTOS”. PARA LAS ECUACIONES TRASCENDENTES, FUERA DE LAS TRIGONOMÉTRICAS O COMBINACIONES FÁCILES DE ELLAS Y ALGUNAS OTRAS ES FÁCIL ENCONTRAR SUS RAÍCES, LAS DEMÁS SOLO PUEDEN RESOLVERSE POR MÉTODOS DE APROXIMACIONES SUCESIVAS. CARACTERÍSTICAS DE LOS MÉTODOS DE APROXIMACIONES SUCESIVAS SE ENTIENDE POR MÉTODO DE APROXIMACIONES SUCESIVAS ÁQUEL, QUE A PARTIR DEL CONOCIMIENTO APROXIMADO DE UNA RAÍZ O CERO DE UNA FUNCIÓN, NOS ACERCA O SATISFACE APROXIMADAMENTE A LA SOLUCIÓN, MEDIANTE LA APLICACIÓN REPETIDA DE UNA ECUACIÓN, LLAMADA DE RECURRENCIA, QUE ES LA QUE DEFINE AL MÉTODO. • LAS CARACTERÍSTICAS SON LAS SIGUIENTES: A) REQUIEREN DE UN VALOR APROXIMADO A SU SOLUCIÓN.(VALOR INICIAL = x0 ) B) SE MEJORA EL VALOR INICIAL APLICANDO SU ECUACIÓN DE RECURRENCIA TANTAS VECES COMO SE REQUIERA. C) NO SON “EXACTOS” • METODO DE BISECCIÓN • SEA UNA FUNCIÓN F(X) = 0, CONTÍNUA, DE VALORES REALES, ALGEBRAICA O TRASCENDENTE, DE LA CUAL SE DESEA CONOCER UN CIERTO VALOR TAL QUE SE CUMPLA QUE F ( ) 0 • EL MÉTODO ESTABLECE QUE SI F(x) ES CONTÍNUA, EN UN INTERVALO (a,b) • Y SE CUMPLE QUE F(a) * F(b) < 0 EXISTIRÁ ENTONCES UN VALOR ADEMÁS SI SE CUMPLE TAL QUE F ' ( ) 0 • POR EL TEOREMA DE ROLLE ESTE VALOR ÚNICO EN (a,b). F() 0; ES EL MÉTODO PROPONE: x 0 COMO ab 2 1) DETERMINAR 2) VALUAR LA FUNCIÓN EN 3) SI AL CALCULAR F( x 0 ) RESULTA DIFERENTE DE CERO IMPLICA QUE NO ES x0 RAÍZ. 4) LA SEGUNDA APROXIMACIÓN SE CALCULA POR LA MEDIA DE x0 , b TOMANDO a, x0 O ÁQUEL EN CUYOS EXTREMOS LA FUNCIÓN TENGA SIGNOS OPUESTOS Y SE REPITE A PARTIR DE EL PASO 3. 5) LA APLICACIÓN SE TERMINA CUANDO TANTO EL ERROR ABSOLUTO COMO EL RELATIVO SON MENORES O IGUALES A LA TOLERANCIA PRESTABLECIDA DE ANTEMANO. Y SE CUMPLE QUE lim x n n EJEMPLO 1 Encuentre una raíz de la siguiente ecuación: 2sen(x) ‐ x =0 Para una tolerancia de 0.007 EJEMPLO 2. Obtenga el valor de “x” para el siguiente problema con tres cifras significativas, sabiendo que el área del trapecio es de 10 metros cuadrados. • • • MÉTODO DE LA REGLA FALSA • CONSIDEREMOS UNA FUNCIÓN F(x) = 0, CONTÍNUA EN UN INTERVALO (a , b) (FALSA POSICIÓN, REGULA FALSI) TAL QUE SE CUMPLA QUE F( ) = 0. • ESTE MÉTODO ES UNA ALTERNATIVA AL MÉTODO DE BISECCIÓN BASADA EN UNA VISUALIZACIÓN GRÁFICA. • CONSISTE EN UNIR CON UNA LÍNEA RECTA LOS VALORES DE LA FUNCIÓN (DEL INTERVALO (a,b)) TAL COMO SE MUESTRA A CONTINUACIÓN. • DE LA FIGURA, POR TRIÁNGULOS SEMEJANTES NOS QUEDA : • EL MÉTODO TERMINA DE APLICARSE CUANDO LOS ERRORES ABSOLUTO Y RELATIVO SON MENORES O IGUALES A LA TOLERANCIA PRESTABLECIDA DE ANTEMANO. • LOS VALORES EN LA APLICACIÓN DE ESTE MÉTODO SE SELECIONAN IGUAL QUE EN BISECCIÓN, DONDE LA FUNCIÓN CAMBIA DE SIGNO, ESTO CON EL FIN DE GARANTIZAR LA CONVERGENCIA. • UNA VARIANTE DEL MÉTODO DE LA REGLA FALSA ES EL DE LA SECANTE, EL CUÁL NO GARANTIZA LA CONVERGENCIA, YA QUE LOS VALORES DE APLICACIÓN SE SELECIONAN ENTRE LOS DOS ÚLTIMOS CALCULADOS. • EJEMPLO 1. • Encuentre una raíz de • • Para una tolerancia ≤ 0.0005 • • EJEMPLO 2. Se va a diseñar un tanque esférico para almacenar agua, el volumen del líquido que puede contener se calcula con v h • • 2 3 R h 3 Donde V = volumen (m3), h = profundidad del agua en el tanque (m), y R = radio del tanque (m). Si R= 3 m ¿ a que profundidad debe llenarse el tanque de modo que contenga 30 m3 ?, para una tolerancia de 0.005. MÉTODO DE NEWTON RAPHSON. (método de las tangentes) SEA UNA FUNCIÓN F(X) = 0, CONTÍNUA EN UN INTERVALO (a, b), CON DERIVADAS , SE PUEDE DESARROLLAR EN SERIE DE TAYLOR PARA OBTENR EL VALOR DE xn ALREDEDOR DEL PUNTO xn 1 . f (xn1 ) f (xn ) f ´(xn )(xn1 xn ) f ´´(xn )(xn1 xn ) ... 1! 2! • EXISTIRÁ UN CIERTO VALOR EN EL INTERVALO • • TOMANDO LOS DOS PRIMEROS TÉRMINOS DE LA SERIE, SE TIENE ( x n , x n 1 ) f (xn1) f (xn ) f ´(xn )(xn1 xn ) • SI ES EL VALOR BUSCADO, ENTONCES: ( x n 1 ) • EN SU INTERSECCIÓN CON EL EJE “X” SE TENDRÁ: x n 1 0 f (xn ) f ´(xn )(xn1 xn ) f (xn ) xn1 xn f ´(xn ) • LA ECUACIÓN ANTERIOR DEFINE AL MÉTODO. • MÉTODO DE LAS TANGENTES • UNA FORMA GRÁFICA DE OBTENER LA ECUACIÓN DE RECURRENCIA ES LA SIGUIENTE. • CONSIDEREMOS UNA FUNCIÓN F(x)=0 CONTÍNUA EN UN INTERVALO (a,b). • • EJEMPLO 1. • Aplique el Método de Newton‐Raphson, para encontrar una raíz, si existe, de la siguiente ecuación: • • • Para una tolerancia menor o igual a 0.001 EJEMPLO 2. Obtenga la raíz cuadrada de 10, utilizando el método de Newton‐ Raphson para una tolerancia menor o igual a 0.0005 TAREA 2. 1. EN LA FUNCIÓN f(x) = sen(x) + 0.5 AL UTILIZAR EL MÉTODO DE , EN LA PRIMERA NEWTON-RAPHSON CON UNA APROXIMACIÓN ITERACIÓN EL VALOR APROXIMADO PARA =3.66, DETERMINE EL CON TRES CIFRAS DECIMALES, VALOR DE LA APROXIMACIÓN INICIAL CONSIDERANDO REDONDEO, UTILICE LOS MÉTODOS DE BISECCIÓN Y SECANTE. 2.ENCUENTRE UNA RAÍZ PARA t ≤ 0.005, POR LOS MÉTODOS DE BISECCIÓN, SECANTE Y NEWTON-RAPHSON PARA LAS SIGUIENTES ECUACIONES 2. 2 5 0 HAGA UNA TABLA COMPARATIVA DE LOS RESULTADOS.