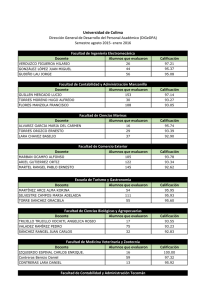
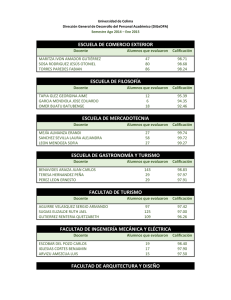
k•e-λ •λk λ•e-λ λ•e-λ λ•e-λ
Anuncio

SOLUCIÓ AL PROBLEMA PROPOSAT AL VOLUM 25 N. 1 PROBLEMA N. 88 Admitiendo que el número X de artı́culos evaluados por cada experto sigue la distribución de Poisson λk fλ (k) = e λ k = 0; 1; 2; : : : k! como sólo tenemos datos de los expertos que evaluaron algún artı́culo, debemos considerar la distribución de X condicionada a X > 0, es decir fλ (k=X > 0) = e λ λk (1 e λ)k! k = 1; 2; : : : El valor medio de esta variable es ∞ µ = = La probabilidad de X =1 ke ∑ (1 k=1 λe (1 e λ e λ λ) λk λ )k! eλ = = λe (1 e λ 1 e condicionada a X p(λ) = > λk λ ) ∑ (k k=1 1 1 )! : 0 es λe 1 e La probabilidad de X = 1 condicionada a X frecuencias siguientes: a = 80 b = 66 λ ∞ λ > λ λ p(λ). Hemos observado las 0 es 1 expertos que evaluaron un artı́culo, expertos que evaluaron más de un artı́culo. A fin de estimar λ, la función y la ecuación de verosimilitud son: L = p(λ)a (1 ln L = a ln p(λ) + b ln (1 ∂ ln L ∂λ = a p 0 (λ ) p (λ ) 369 p(λ))b p(λ)) b p0 (λ) (1 p(λ)) =0 Como p0 (λ) > 0 para todo λ > 0, la ecuación se reduce a a p(λ) La solución de la ecuación (1 b p(λ)) λe 1 e ) =0 λ λ = p (λ ) = a : a+b 80 80 + 66 es λ̂ = 1:10. La estimación máximo verosı́mil de µ es µ̂ = λ̂ 1 e λ̂ = 1:65 Respuesta: los expertos (referees) consultados por Qüestiió (1987-1997) evaluaron, por término medio, 1.65 artı́culos cada uno. C.M. Cuadras Universitat de Barcelona 370