Efecto de la compresibilidad de los gases durante el control de una
Anuncio

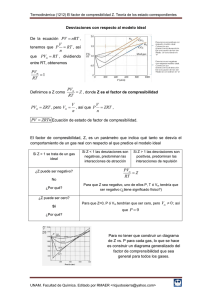
Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Ing. Hugo Mocchiutti Ing. Tomás Catzman Pan American Energy Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Índice Comportamiento de los Gases Método Volumétrico Control de Pozo Evolución del Gas Ideal vs Gas Real Hipótesis de Resolución Aplicación en un Pozo Conclusiones Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Comportamiento de los Gases Diagrama de Fases P-T (Sustancia Pura) *Gráficas obtenidas de la base de datos de imágenes de “Google” Diagrama de Fases P-T (Mezcla) Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Comportamiento de los Gases Gases Ideales 1° Boyle: El volumen de una cantidad determinada de gas es inversamente proporcional a su presión p x V = cte 2° Charles: El volumen y la temperatura de una cantidad determinada de gas son directamente proporcionales p / T = cte 3° Avogadro: El volumen de una gas ideal no sólo depende de la temperatura y la presión, sino que del número de moléculas o de moles de dicho gas, sin importar el tipo de molécula o la composición del gas. p.V=n.R.T Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Comportamiento de los Gases Gases Reales Tiempo después, en situaciones donde las magnitudes de la presión y la temperatura eran considerablemente mayores, se observó en el gas una diferencia entre el comportamiento teórico y el real. A la cuantificación de dicho desvío se la llamó “factor de desviación z”, comúnmente llamado “factor de compresibilidad z” p.V=z.n.R.T Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Comportamiento de los Gases Gases Reales Factor de Compresibilidad “Standing & Katz” Factor de Compresibilidad “Kvalnes & Gaddy” *Gráficas obtenidas de la base de datos de imágenes de “Google” y del libro Advanced Well Control - SPE Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Comportamiento de los Gases Gases Reales “Se introduce un error bastante significativo al depender de un método de resolución gráfico. A esto se le suma la incomodidad que implica la utilización del mismo” Dranchuk & Abou Kassemm z = 1 + c1(TPR).pr + c2(TPR).pr2 - c3(TPR).pr3 + c4(pr,TPR) 0.2 < pPR < 30 1.0 < TPR < 3.0 donde: pr = 0.27 . pPR/(z . TPR) c1(TPR) = A1 + A2/TPR + A3/TPR3 + A4/TPR4 + A5/TPR5 c2(TPR) = A6 + A7/TPR + A8/TPR2 c3(TPR) = A9 . (A7/TPR + A8/TPR2) c4(pr,TPR) = A10 . (1 + A11 . pr2).(pr2/TPR3) . exp (-A11 . pr2) A1 = 0.3265 A2 = -1.0700 A3 = -0.5339 A4 = 0.01569 A5 = -0.05165 A6 = 0.5475 A7 = -0.7361 A8 = 0.1844 A9 = 0.1056 A10 = 0.6134 A11 = 0.7210 Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Comportamiento de los Gases Simplificaciones Inexactas “La industria de perforación ha simplificado la ley de gas de Boyle a lo siguiente : P1 * V1 = P2 * V2 donde P1 es la presión de una burbuja de gas a condiciones iniciales, V1 es el volumen de la burbuja de gas a condición inicial, P2 es la presión a otra condición diferente a la inicial y V2 es el volumen a esa nueva presión …” “… By neglecting changes in temperature, T, and compressibility factor, z, the equation can be simplified into… P1.V1 = P2.V2” “… la Ley de los Gases Perfectos puede ser considerada suficientemente precisa como para tenerse en cuenta en el caso de la migración del gas en los pozos…” Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Control de Pozo Presión de Casing (Método Volumétrico) Presión de Fondo (Método Volumétrico) *Gráficas obtenidas del libro Advanced Well Control - SPE Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Gases Ideales PC Dg hg D * P . V = n . R . T = cte P 1 . V1 = P2 . V2 Pg2 V2 * PC = Pg - 0.052 . dlodo . Dg Dg = Pg – PC 0.052 . dlodo * Phg = 0.052 . dgas . hg Pg1 V1 * Pfdo = 0.052 . dlodo . (D – hg) + Phg Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Gases Reales *P.V=z.n.R.T PC Dg hg D Pg2 V2 T2 Z2 P1 . V 1 = P 2 . V 2 z1 . T1 z2 . T2 * PC = Pg - 0.052 . dlodo . Dg Dg = Pg – PC 0.052 . dlodo * Phg = 0.052 . dgas . hg Pg1 V1 T1 Z1 Phg = 0.052 . gg . Pg . hg 2.77 . z . T * Pfdo = 0.052 . dlodo . (D – hg) + Phg Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Hipótesis de Resolución A) Incremento Presión de Trabajo: “Mientras la PC incrementa hasta alcanzar la presión de trabajo, el gas migra a volumen constante, y asumiendo que no hay intercambio de calor (debido al corto tiempo de exposición), la presión no varía. La nueva Dg queda definida por la columna de lodo equivalente al diferencial de presión” Dg = Pg – PC 0.052 . dlodo Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Hipótesis de Resolución B) Purga de Lodo (gases ideales): Una vez alcanzada la presión de trabajo se comienza a purgar el volumen de lodo necesario para que la presión en el fondo del pozo disminuya en un diferencial igual al recientemente incrementado. Dicha maniobra se realiza a PC constante. El gas se expande hasta ocupar el volumen del lodo purgado. Para poder determinar la posición exacta de la burbuja se debe partir de los datos “duros” (PC, volumen del gas) y realizar una iteración doble hasta hallar una convergencia. Datos: Pg hg Pg1.hg1 hg2 Una vez definida la nueva presión, se calcula la posición del tope de la burbuja Pg2 Dg2 Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Hipótesis de Resolución B) Purga de Lodo (gases reales): Una vez alcanzada la presión de trabajo se comienza a purgar el volumen de lodo necesario para que la presión en el fondo del pozo disminuya en un diferencial igual al recientemente incrementado. Dicha maniobra se realiza a PC constante. El gas se expande hasta ocupar el volumen del lodo purgado. A su vez el gas sigue migrando variando su presión y temperatura. Para poder determinar la posición exacta de la burbuja se debe partir de los datos “duros” (PC, volumen del gas) y realizar una iteración doble hasta hallar una convergencia. Phg = 0.052 . gg . Pg . hg 2.77 . z . T Dg = Pg – PC 0.052 . dlodo Pg = 53.29 . Phg . T z gg . Hg PPR = P / PPC TPR = T / TPC Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Hipótesis de Resolución B) Purga de Lodo (gases reales): Datos: gg Phg hg T Utilizando el P/z Proponiendo un z P z P PPR z TPR Una vez que z converge se define P, con este último dato, la densidad del lodo y la PC se calcula el tope de la burbuja La primera vez se utiliza la T del fondo Dg Una vez obtenida la nueva T se repite la primera iteración para obtener los nuevos z y P. Este proceso se repite hasta la convergencia de T Con la profundidad de la burbuja y un gradiente de temperatura conocido se calcula la nueva T T Dg Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Aplicación en un pozo Datos: Profundidad (D): 19400 pies Diámetro pozo: 7 7/8” dlodo: 16 ppg Preservorio: 16136 psi T = 100°F + 1.5 °F/100 pies Ganancia en pileta: 100 bbl SICP (PC1): 2300 psi ggas: 0.6 hgas = Vgas / Areapozo hgas = 100 bbl / 0.34 pies2 . 5.61 pies3/bbl hgas = 1660 pies T = 100 °F + 1.5 °F * 19400 pies/100 pies T = 391 °F = 851 °R PPR = 16136 psi / 677 = 23.83 TPR = 851°R / 352 = 2.42 z = 1.697 Phg = 0.052 . gg . Pg . Hg 2.77 . z . T Phg = 0.052 . 0.6 . 16136 psi . 1660 pies 2.77 . 1.697 . 851 °R Phg = 209 psi Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Aplicación en un pozo Presión de Fondo (real) 17600 17600 17550 17550 17500 17500 17450 17450 Presión [psi] Presión [psi] Presión de Fondo (ideal) 17400 17350 17400 17350 17300 17300 17250 17250 17200 17200 0 5 10 15 Paso 20 25 30 0 2 4 6 Paso 8 10 Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Aplicación en un pozo Presión de Casing (real) 5200 5200 4700 4700 4200 4200 Presión [psi] Presión [psi] Presión de Casing (ideal) 3700 3700 3200 psi 3200 3200 2700 2700 2200 5200 psi 2200 0 5 10 15 Paso 20 25 30 0 5 10 15 Paso 20 25 30 Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Aplicación en un pozo Presión de Casing [psi] 2300 0 2800 3300 3800 4300 4800 5300 2000 4000 Evolución del Gas en el Pozo Profundidad [pies] 6000 8000 Real 10000 12000 14000 16000 18000 Ideal Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Método Volumétrico Aplicación en un pozo Pasos Presión de Casing (máx) Presión de Fondo (máx) Volumen de Gas (inicial) Volumen de Gas (máx) Calculos Realizados IDEAL 29 5300 psi 17470 psi 100 bbls 304 bbls 60 REAL 9 3300 psi 17466 psi 100 bbls 159 bbls 170 Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Conclusiones Considerar un gas como ideal puede llegar a traer errores de diseño que impacten en aspectos tanto de seguridad como económicos. El error que puede aparecer por calcular la evolución de un gas de manera incorrecta puede llevar a una mala elección del método de control de pozo a utilizar. Si el diseño de cañería ya está establecido, la diferencia entre calcular de una forma u otra llevaría a seleccionar una menor tolerancia de ingreso de gas al pozo. Debido a las múltiples variables que afectan la evolución del gas en un pozo (las mencionadas en esta presentación y otras) es altamente recomendable hacer el diseño de cañería y de control de pozos utilizando un simulador, planteando distintas alternativas que pudieran ocurrir. Debemos estar seguros que este último trate el gas como real. Efecto de la Compresibilidad de los Gases durante el Control de una Surgencia Bibliografía Consultada Advanced Apuntes Well Control – SPE Petrofísica y Fluidos de Reservorios (ITBA) – Juan Rosbaco Drilling Data Handbook – IFP Blowout and Well Control Handbook – Robert D Manual Well Control – UN Cuyo Manual Well Control – San Antonio Manual Well Control – Chevron Manual Well Control – ENI