El mecanismo de la ley de D`Hondt
Anuncio
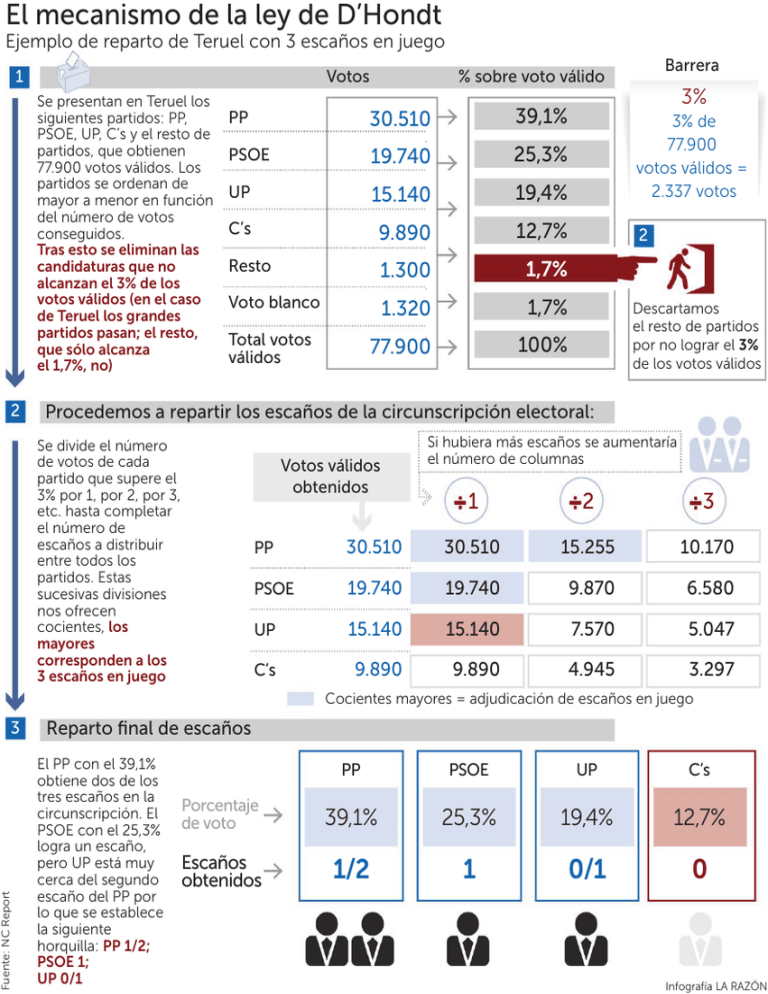
El mecanismo de la ley de D’Hondt Ejemplo de reparto de Teruel con 3 escaños en juego Se presentan en Teruel los siguientes partidos: PP, PSOE, UP, C’s y el resto de partidos, que obtienen 77.900 votos válidos. Los partidos se ordenan de mayor a menor en función del número de votos conseguidos. Tras esto se eliminan las candidaturas que no alcanzan el 3% de los votos válidos (en el caso de Teruel los grandes partidos pasan; el resto, que sólo alcanza el 1,7%, no) 2 Barrera % sobre voto válido Votos 1 3% PP 30.510 39,1% PSOE 19.740 25,3% UP 15.140 19,4% 3% de 77.900 votos válidos = 2.337 votos C’s 9.890 12,7% 2 Resto 1.300 1,7% Voto blanco 1.320 1,7% 77.900 100% Total votos válidos Descartamos el resto de partidos por no lograr el 3% de los votos válidos Procedemos a repartir los escaños de la circunscripción electoral: Se divide el número de votos de cada partido que supere el 3% por 1, por 2, por 3, etc. hasta completar el número de escaños a distribuir entre todos los partidos. Estas sucesivas divisiones nos ofrecen cocientes, los mayores corresponden a los 3 escaños en juego Votos válidos obtenidos Si hubiera más escaños se aumentaría el número de columnas 1 2 3 PP 30.510 30.510 15.255 10.170 PSOE 19.740 19.740 9.870 6.580 UP 15.140 15.140 7.570 5.047 C’s 9.890 9.890 4.945 3.297 Cocientes mayores = adjudicación de escaños en juego Fuente: NC Report 3 Reparto final de escaños El PP con el 39,1% obtiene dos de los tres escaños en la circunscripción. El PSOE con el 25,3% logra un escaño, pero UP está muy cerca del segundo escaño del PP por lo que se establece la siguiente horquilla: PP 1/2; PSOE 1; UP 0/1 PP PSOE UP C’s Porcentaje de voto 39,1% 25,3% 19,4% 12,7% Escaños obtenidos 1/2 1 0/1 0 Infografía LA RAZÓN